UNEC Journal of Engineering and Applied Sciences Volume 5, No 2, pages 27-44 (2025) Cite this article, 380 https://doi.org/10.61640/ujeas.2025.1203
The adoption of variable-speed wind turbines (VSWTs) has garnered considerable interest as a viable and sustainable source of renewable energy [1]. This is attributed to their capacity to capture wind energy from any direction and their compact design, rendering them particularly appealing for diverse applications, including urban settings. Nevertheless, the intricate aerodynamic and mechanical attributes of VSWTs introduce substantial challenges when it comes to ensuring their dependable and effective operation [2-11]. Among these challenges, the control of VSWTs in different regions to achieve specific objectives stands out as particularly critical due to its high degree of nonlinearity. The VSWT has four operational regions, including the regions with low-speed (Region-I), medium-speed (Region-II), high-speed (Region-III), and furling speed (Region-IV), respectively, as shown in figure 1. The VSWT is stopped until the cut-in wind speed is reached in Region-I, then operates at a constant tip-speed ratio to maximize the power coefficient in Region-II. The VSWT operates at a lower power coefficient in Region-III and remains shut down after the cut-out wind speed
in Region-IV [12].
Numerous researchers have contributed to the field of control applications of VSWT in various studies [1-13]. Some researchers have proposed the use of a proportional-integral-derivative (PID) controller to maximize power output in the torque control region, while others have applied a PID-based pitch control scheme to achieve a constant power output [5]. To obtain the output power in a wind energy conversion system (WECS), it is crucial to measure the peak power with the aid of a maximum power point tracking (MPPT) controller, which is essential for any type of generator in use [6]. In situations with significant fluctuations in wind speed, a controller that tracks the MPP around the operational region is needed to increase the energy a wind turbine produces. The ideal generator speed must be determined to achieve the maximum energy output feasible, regardless of wind speed. This MPPT method is typically utilized when wind speeds are between certain ranges [7]. However, wind turbine models have a high degree of uncertainty and disturbance due to changing wind speeds, tower dynamics, nacelle dynamics, pitch angle, and other factors, making control of the wind turbine more challenging. Therefore, developing a control law that can maintain system functionality despite major interruptions is crucial [8].
A range of both traditional and unconventional control methods is employed to provide robustness to control systems design [9-12]. In the case of actual dynamic systems, performance would inevitably be impacted by unmodeled dynamics, parameter drifts, uncertainties, and external disturbances, making precise disturbance rejection a major goal for modern closed-loop control industrial systems [12]. Although proportional-integral-derivative (PID) control is commonly used, its performance is limited due to the need for adaptive tuning [13]. An optimal controller based on model predictive control has been proposed for the torque and pitch control regions of the VSWT, which works well but is highly dependent on cost-weight function optimization [15]. Quantitative feedback theory (QFT) in robust control is unsuitable for more complex wind turbine systems because it necessitates a thorough mathematical understanding of the system. Although linear approaches based on QFT have been studied for the two-mass VSWT model, their stability is only local and may be compromised by unstructured perturbations and uncertainty [16].
Various studies have explored nonlinear control strategies aimed at optimizing the power output of wind turbines [17-28]. For instance, backstepping control has been applied to VSWTs, while feedback linearization techniques have been used to control pitch under nonlinearities and uncertainties [17-18]. The sliding mode control (SMC) algorithm offers another avenue for enhancing VSWT and controller resilience. This is evident in the utilization of a high-order optimum scheme to craft a fractional terminal SMC-based controller, intending to maximize energy capture and minimize mechanical loads. Researchers have even utilized a homotopy singular perturbation technique to devise an SMC-based control approach for wind turbines [19]. This study introduces a robust control design technique to elevate the performance of VSWT operations.
The inherent model of VSWT is often influenced by unknown factors such as tower vibrations, friction, and uncertain wind speeds, posing challenges for precise measurement. Consequently, the proposed approach integrates a nonlinear feedback control alongside a modified uncertainty disturbance estimator [20] with particle swarm optimization (PSO) based tuning of controller parameters to attain robust VSWT performance [29]. The simulation study validates the efficacy of the recommended nonlinear control method, showcasing improved operational efficiency and satisfactory robustness of the VSWT when faced with internal and external uncertainties compared to the standard wind turbine controller.
Additionally, it has been demonstrated that the controller recommended in this study outperforms (i) a standard wind turbine controller (SWTC) [15], (ii) a proportional-integral (PI) controller [13], and (iii) a QFT-based controller [23]. The proposed control scheme is based on a modified formulation of the approach presented in [29]. The approach has been extended to the rotor speed control problem with matched uncertainty. The proposed control formulation has required only the output, whereas [21,29] considered the control reliant on all the state variables. This simplification shows the reduction in complexity during the proposed scheme implementation.
The major highlights of the contributions of this paper are as follows: (i) an ellipse-based design is presented to guarantee the boundedness of VSWT inputs subjected to the input constraints; (ii) the suggested controller eliminates the requirement for the strict assumptions found in earlier designs by inheriting the robustness of traditional approaches and offering precise instructions for parameter choices; (iii) integral windup is prevented by adding a second time-varying variable to the error dynamics, which gets closer to zero as the controller output gets closer to its limits; (iv) the development of a dynamic controller with a boundedness design guarantees that the time-varying variable and the controller output remain inside the specified ellipse; (v) the obtained results demonstrate the boundedness, stability, and performance analysis compared to conventional UDE-based controller and other controllers to show the proposed design's effectiveness.
The structure of the manuscript is outlined in the following way. Section 2 presents the dynamical model of the VSWT. The control goals are defined in section 3, whereas section 4 describes the development of the robust controller using the BUE and PSO approach. The stability of the proposed method is analyzed in section 5. Finally, the results of the robust controller based on the BUE design are discussed in Section 6, followed by the conclusions in the last section.
The dynamic model of a VSWT comprises aerodynamic, rotor mechanics, tower, and electrical generator models. Rotor blades transform wind kinetic energy into mechanical energy through aerodynamic torque, transferring it to the generator through a gearbox. The tower's movement influences the perceived wind speed of the rotor, calculated by considering tower velocity and actual wind speed. Pitch and torque actuation models optimize rotor speed for maximum power extraction, and pitch actuation adjusts blade angle to control aerodynamic torque, while generator actuation applies an electrical counter torque for power extraction.
The VSWT model expressed in the above equations can be represented by a block diagram below (figure 2).
2.1 Mechanical Model of VSWT
The VSWT system has been mechanically modeled using differential equations in references [15,24].
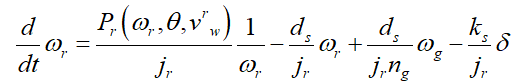 (1)
(1)
where
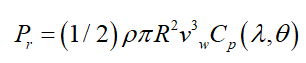 (2)
(2)
where
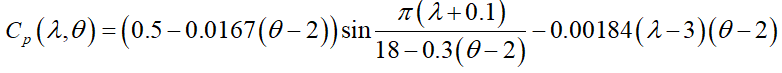 (3)
(3)
where
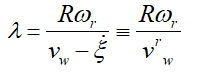 (4)
(4)
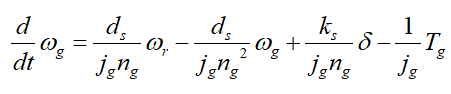 (5)
(5)
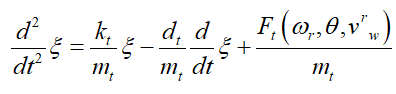 (6)
(6)
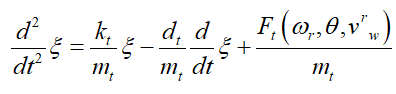 (7)
(7)
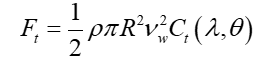 (8)
(8)
where
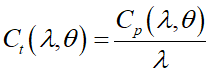 (9)
(9)
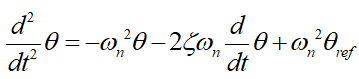 (10)
(10)
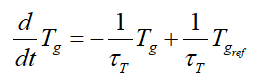 (11)
(11)
2.2 State-Variable Model of VSWT
The dynamical equations of the VSWT model given in (1)-(11) can be rewritten as,
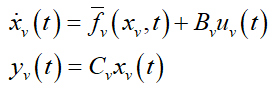 (12)
(12)
where

and
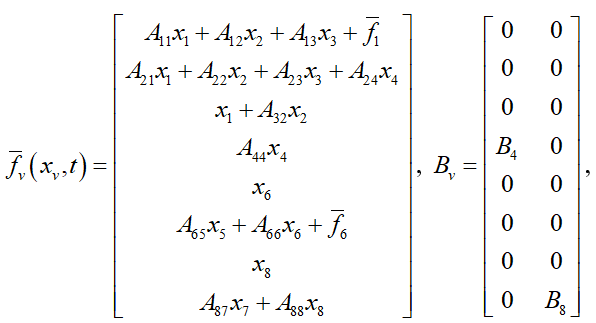
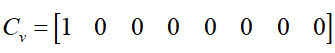
Where
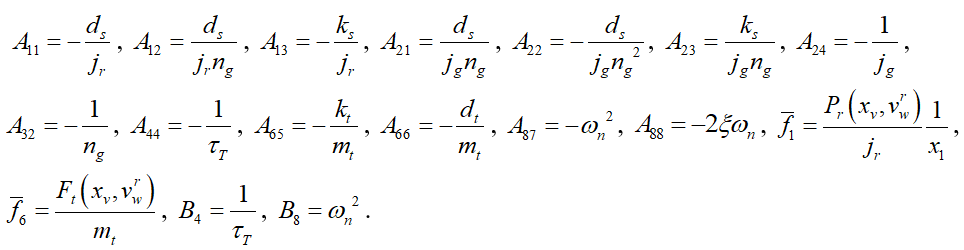
This section introduces the problem statement for the development of a robust controller of VSWT for the torque and pitch control regions. In the region of torque control (RTC), the optimal value of tip-speed ratio can be calculated to extract maximum power (by varying the generator torque where the pitch angle remains constant) as,
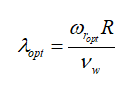 (13)
(13)
and the maximum power can be obtained at a peak point 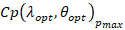 .
.
Similarly, in the region of pitch control (RPC), the rated/nominal value of power can be obtained to achieve invariable power (by varying the pitch angle, where generator torque remains constant) as
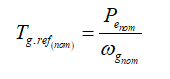 (14)
(14)
3.1 Uncertain Model of VSWT
The plant model (9) with uncertainty can be stated as,
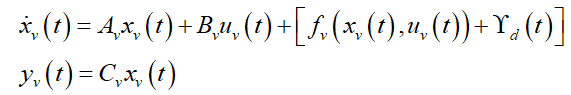 (15)
(15)
where 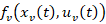 is the nonlinearity of the VSWT plant, along with uncertainty,
is the nonlinearity of the VSWT plant, along with uncertainty, 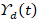 represents the bounded disturbance as
represents the bounded disturbance as 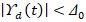 . The second term of (13) represents the matched uncertainty presented in the VSWT plant, which is defined as
. The second term of (13) represents the matched uncertainty presented in the VSWT plant, which is defined as 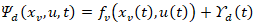 . Also, the plant input is subjected to the interval constraint
. Also, the plant input is subjected to the interval constraint 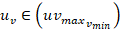 .
.
3.2 Control Objectives
The purpose of this study is to create a BUE-based robust controller for VSWT that has the following features.
(i) The measured rotor speed approaches the reference model, which corresponds to the rated rotor speed for RPC and the optimal rotor speed for RTC.
(ii) The tracking error of the plant's output state and the reference model asymptotically approaches zero.
(iii) Subject to interval restrictions on the torque and pitch control input variables, the tracking performances satisfy the plant input.
(iv) The utmost power output achievable from the prevailing wind conditions
To achieve the aforementioned goals, a robust controller architecture has been developed, and it will be described in more detail in the following section.
The UDE design approach [20] has been expanded here to account for both matched uncertainty and the affine system since the VSWT model (15) is affine. A stable and strictly proper filter is taken into consideration.
4.1 Design of reference model
The settings of the parameters to extract the most power from the available wind are provided by the dynamic characteristics of a certain VSWT. The aero-dynamical model (3) can be used to determine this. According to figure 3, the 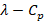 characteristic for the VSWT (22) has been computed.
characteristic for the VSWT (22) has been computed.
The aforementioned curve at 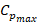 =0.55 yields the value of
=0.55 yields the value of 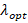 = 9.5 (figure 3). As a result, the reference model with the requisite characteristics has been determined to be the optimal rotor speed [24],
= 9.5 (figure 3). As a result, the reference model with the requisite characteristics has been determined to be the optimal rotor speed [24],
For RTC
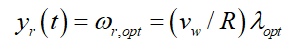 (16)
(16)
For RPC
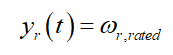 (17)
(17)
4.2 Uncertainty Disturbance Estimator (UDE)-Based Robust Controller Design [20]
Consider a filter 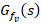 that is stable, rigorously proper, and has a gain of unity and a phase-shift of zero over the range of
that is stable, rigorously proper, and has a gain of unity and a phase-shift of zero over the range of 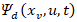 . Consequently, the unknown phrase can be
. Consequently, the unknown phrase can be 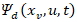 approximately described as,
approximately described as,
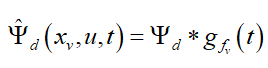 (18)
(18)
where symbol * represents the convolution operator and 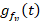 is the impulse response of the low-pass filter
is the impulse response of the low-pass filter 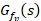 given by
given by
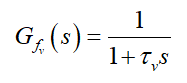 (19)
(19)
where 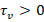 ensures the filter's bandwidth and covers the spectrum of
ensures the filter's bandwidth and covers the spectrum of 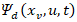 .
.
The reference and plant output tracking error is considered as, 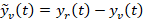 , whereas the dynamics of tracking error are assumed to be
, whereas the dynamics of tracking error are assumed to be
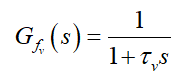 (20)
(20)
The tracking error dynamics are given by,
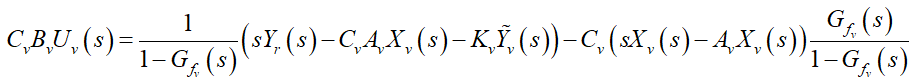 (21)
(21)
and the UDE-based control law [20] is given as,
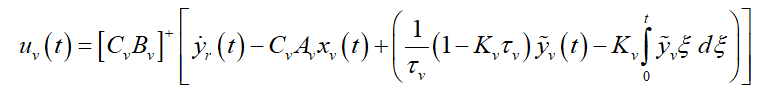 (22)
(22)
where
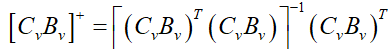
The control law (22) is a combined controller that relies on uncertainty estimation. It is considered robust because the control signal 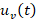 has been constructed using an estimate of uncertainty, which includes nonlinearity, parametric variation, and disturbances. Figure 4 depicts the block diagram of the UDE-based robust control of VSWT [20].
has been constructed using an estimate of uncertainty, which includes nonlinearity, parametric variation, and disturbances. Figure 4 depicts the block diagram of the UDE-based robust control of VSWT [20].
The UDE-based controller (20) uses two terms involving the filter design (i) 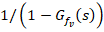 (which always includes integral action) and (ii)
(which always includes integral action) and (ii) 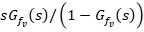 (excludes integral action, because of the
(excludes integral action, because of the 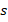 term in the numerator). The filter's role is crucial in estimating uncertainties and disturbances and achieving good control performance [29]. The integral action of the first term is used to achieve tracking performance of the rotor speed. However, if the VSWT plant is subject to interval constraints on inputs, it might cause an integral windup. One solution to this problem is an anti-windup design, as reported in [28]. However, in the proposed work, the boundedness design is considered for developing the proposed control scheme to deal with integral windup, disturbances, and uncertainties.
term in the numerator). The filter's role is crucial in estimating uncertainties and disturbances and achieving good control performance [29]. The integral action of the first term is used to achieve tracking performance of the rotor speed. However, if the VSWT plant is subject to interval constraints on inputs, it might cause an integral windup. One solution to this problem is an anti-windup design, as reported in [28]. However, in the proposed work, the boundedness design is considered for developing the proposed control scheme to deal with integral windup, disturbances, and uncertainties.
4.3 Bounded uncertainty disturbance estimator-based robust controller design:
If the plant inputs are constrained in the robust controller (22) designed for VSWT, the integral windup continuously affects the rotor speed tracking. For the mitigation of this effect, an additional term 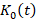 is augmented in the error dynamics (20), given by
is augmented in the error dynamics (20), given by
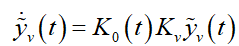 (23)
(23)
where the time-varying term is varying as 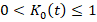 .
.
The error dynamics of VSWT given in (27) and (17) have been compared, resulting in
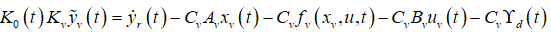 (24)
(24)
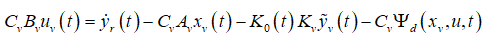 (25)
(25)
Replacing the unknown term 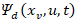 with its estimate (25) results
with its estimate (25) results
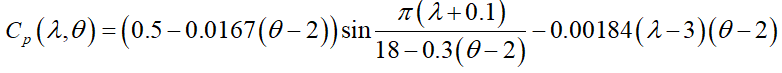 (26)
(26)
Taking the Laplace Transform of (26) gives
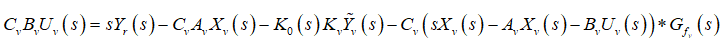 (27)
(27)
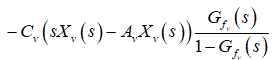 (28)
(28)
Substituting (19) in the expression of (28) results in
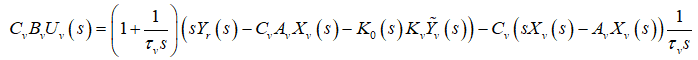 (29)
(29)
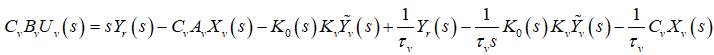 (30)
(30)
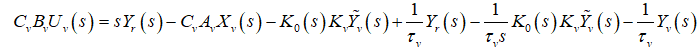 (31)
(31)
where 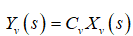 .
.
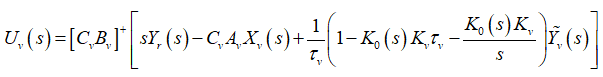 (32)
(32)
Where

Taking the inverse Laplace Transform of (32), the robust control law is obtained as,
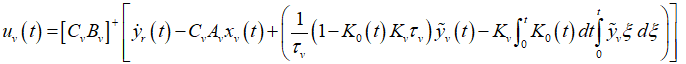 (33)
(33)
Preventing integral windup can be achieved if the additional term 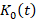 moves toward zero when the above control law (33) approaches the bounds
moves toward zero when the above control law (33) approaches the bounds 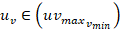 . This condition can be retained if the designed
. This condition can be retained if the designed 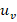 and
and  can always move and remain on an ellipse as depicted in figure 5.
can always move and remain on an ellipse as depicted in figure 5.
The above condition can be expressed as,
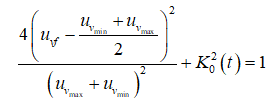 (34)
(34)
Suppose that 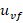 represents the final control element. The desired ellipse (34) can be achieved,
represents the final control element. The desired ellipse (34) can be achieved,
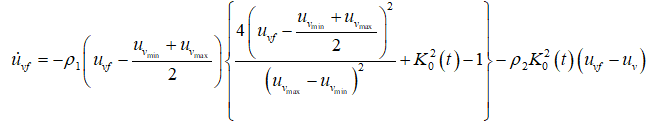 (35)
(35)
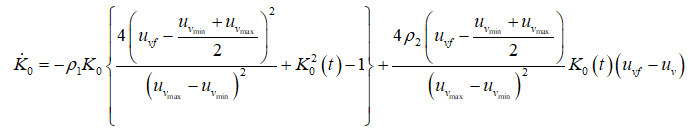 (36)
(36)
where 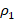 and
and 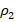 are the positive constants.
are the positive constants.
The VSWT plant order does not affect the boundedness design (35) and (36), which doesn't cost many computational resources. The following Lemma is used to analyse the boundedness of the suggested design (35) and (36).
4.5 Stability analysis
The boundedness of the proposed control law design (35) and (36) with 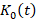 and
and 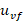 can be regulated within (34), considering the input constraint under the range
can be regulated within (34), considering the input constraint under the range 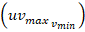 .
.
Considering the Lyapunov function candidate as follows,
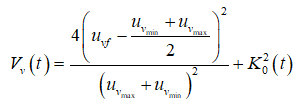 (37)
(37)
The derivative of (37), along with (35) and (36), yields
 (38)
(38)
The solution of the above differential equation can be obtained as,
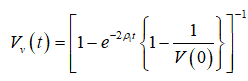 (39)
(39)
During the design of 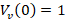 initially with
initially with 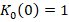 and
and 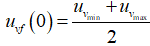 , results
, results 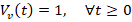
According to expression (37), it always holds the expression (34), and the final control element remains within the range 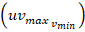 .
.
Remarks:
For the proposed BUE-based robust control design (figure 6), the trajectory of the 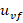 and
and 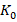 will start and remain on the ellipse (34), disregarding the changes in the final control element. Expressions (35) and (36) will regulate to zero when the rotor speed tracking error tends to zero. Thus,
will start and remain on the ellipse (34), disregarding the changes in the final control element. Expressions (35) and (36) will regulate to zero when the rotor speed tracking error tends to zero. Thus, 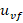 and
and 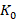 converge to the equilibrium points (
converge to the equilibrium points (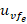 and
and 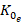 ), when
), when 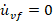 and
and 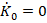 . The average of the confined interval is started in boundedness design and Lyapunov theory-based analysis for dealing with more general interval input constraint after comparing the schemes, are shown in section 5.
. The average of the confined interval is started in boundedness design and Lyapunov theory-based analysis for dealing with more general interval input constraint after comparing the schemes, are shown in section 5.
4.6 Optimization of controller parameters
In this study, PSO is employed to optimally tune the design parameters of the proposed controller for VSWT [29]. It is a stochastic, population-based optimization technique inspired by the social behavior of birds and fish. It has become a widely adopted approach for solving nonlinear, high-dimensional, and non-convex optimization problems due to its simplicity, flexibility, and global search capability. The objective is to enhance system robustness and tracking accuracy while minimizing tracking errors. A cost function based on the integral of squared tracking error, control effort, or a multi-objective performance index is defined as the optimization criterion. The PSO algorithm iteratively refines the controller parameters to minimize this cost function under system nonlinearities and parameter uncertainties. By leveraging PSO for controller tuning, the proposed robust control frameworks achieve superior dynamic performance and resilience, which is well-suited for real-time control of a highly unstable VSWT system.
In PSO, a group of candidate solutions, known as particles, traverse the search space to locate the optimum of a given objective function. Each particle adjusts its trajectory based on its own best-known position and the best-known positions of its neighbors. The dynamic adjustment of particle velocity and position is governed by both individual cognition and swarm cooperation, which enables efficient exploration and exploitation of the solution space.
Initialization: Randomly initialize the positions and velocities of all particles in the n-dimensional search space. Set a personal best 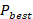 and a global best
and a global best 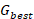 . Define control parameter bounds and maximum iterations.
. Define control parameter bounds and maximum iterations.
Evaluate Fitness: For each particle, compute the fitness using a performance index
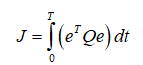 (40)
(40)
where 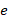 is the state error vector.
is the state error vector.
Update Personal and Global Bests: If the current fitness is better than the previous 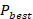 update, it. Update
update, it. Update 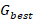 if any particle outperforms the current global best.
if any particle outperforms the current global best.
Update Velocity and Position: The position and velocity of each particle are updated at every iteration according to the following equations.
Update each particle's velocity:
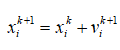 (41)
(41)
Update position:
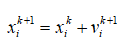 (42)
(42)
where 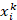 and
and 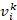 are the position and velocity of the
are the position and velocity of the 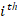 particle at iteration k
particle at iteration k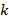 ;
; 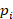 is the personal best position of the particle;
is the personal best position of the particle; 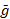 is the global best position among all particles;
is the global best position among all particles;  is the inertia weight;
is the inertia weight; 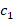 and
and 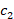 are acceleration coefficients;
are acceleration coefficients; 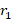 and
and 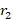 are random numbers uniformly distributed in
are random numbers uniformly distributed in 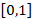 .
.
Boundary Check: Ensure updated positions remain within predefined bounds.
Termination Check: If the maximum number of iterations is reached or the solution converges, terminate; otherwise, go to evaluate fitness.
After analyzing the VSWT system (22) with parameters specified in table 3 [14], [30], a robust control approach for VSWT has been developed (figure 6). The simulations have been carried out using the proposed scheme in MATLAB under different conditions, and the results are presented below. To simulate the VSWT plant with the new control scheme, the following design parameters are selected as listed in table 1.
Figures 7-10 show the tracking performance of VSWT when the suggested robust controller is implemented without taking uncertainty/disturbance and control effort into account. The study presents the results that have been attained. The rotor speed measurements obtained from figure 7a demonstrate that the RTC implementation accurately tracks the reference model (16) of the VSWT system to achieve optimal power. Similarly, the response obtained from the RPC implementation in figure 7b indicates that the measured rotor speed attains the rated value of the rotor speed specified in the reference model (17) for steadily maintaining optimal power. The control inputs of VSWT are depicted in figure 8 for RTC and RPC. Figure 9 reveals that the final control elements (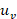 ) are within the actuator limits (i.e.,
) are within the actuator limits (i.e., 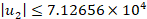 N-m,
N-m, 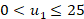 deg) [24]. Also, the time-varying term
deg) [24]. Also, the time-varying term 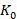 is plotted in figure 10, showing its boundedness in both operating regions. The outcomes support the proposed control scheme's ability to produce precise and efficient performance for the VSWT system without uncertainties.
is plotted in figure 10, showing its boundedness in both operating regions. The outcomes support the proposed control scheme's ability to produce precise and efficient performance for the VSWT system without uncertainties.
Remarks: To test the proposed scheme's effectiveness, it was implemented under various initial conditions and wind trajectories. The same level of performance was consistently achieved in all cases. The proposed control scheme was also assessed for its robustness, and the findings are detailed in the subsequent section of the study. A comparison of the suggested robust control scheme's performance to that of other existing schemes was also done.
The study compared the proposed controller (35) designed specifically for VSWT with three different existing control schemes. These schemes include standard wind turbine control (SWTC) [22], proportional-integral (PI) control [23], and QFT-based control [24]. For each working region (RTC/RPC), a distinct standard control scheme was used, and it is described in the following sections.
(i) SWTC Scheme [22]
The proposed scheme's ability to extract power was compared with SWTC to justify its performance. The RTC SWTC law is presented below.
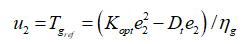 (43)
(43)
where 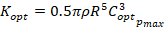 and
and 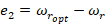
(ii) PI Controller [23]
A standard PI controller was developed, and its performance was compared in order to assess the performance of the proposed controller (35) for RPC. The PI control law for RPC is shown below.
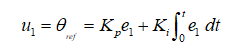 (44)
(44)
where 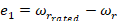 and the PI controller gains
and the PI controller gains 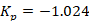 and
and 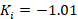 .
.
(iii) QFT-Based Controller [24]
In this study, the QFT control approach, which addresses the needs of RTC and RPC, was employed. The torque control law for RTC based on QFT is shown below.
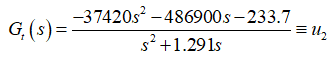 (45a)
(45a)
where 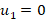 .
.
Similarly, the pitch control law for RPC based on QFT is provided below.
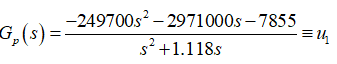 (45b)
(45b)
where 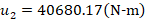 .
.
The results are discussed below, along with the comparative responses that were provided.
As demonstrated in figure 11, the VSWT's tracking performance with the proposed controller is both smoother and faster, resulting in substantial improvement compared to other existing schemes. Additionally, the quality of tracking with the proposed controller is superior, as indicated by the considerably smaller tracking error in comparison to the responses obtained from other existing schemes. In order to evaluate the effectiveness of the proposed control scheme, the impact of parameter uncertainties on the VSWT model has been investigated. The uncertainties range from ±5% to ±15% for both control regions in the VSWT model.
The parameters selected as the affected model parameters are given by, 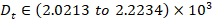 ,
, 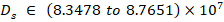 ,
, 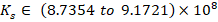 , and
, and 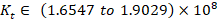 . Additionally, an external disturbance in the VSWT plant has been considered, where the disturbance is represented by
. Additionally, an external disturbance in the VSWT plant has been considered, where the disturbance is represented by  , where
, where 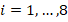 . The performance of the VSWT model under the aforementioned uncertainties has been analyzed through simulation using the proposed control scheme as well as existing control schemes. The simulation results demonstrate that the proposed control scheme outperforms the existing control schemes in terms of performance, although the detailed responses are not presented here due to space limitations. The numerical results of all the responses have been tabulated in table 2.
. The performance of the VSWT model under the aforementioned uncertainties has been analyzed through simulation using the proposed control scheme as well as existing control schemes. The simulation results demonstrate that the proposed control scheme outperforms the existing control schemes in terms of performance, although the detailed responses are not presented here due to space limitations. The numerical results of all the responses have been tabulated in table 2.
Using root-mean-square (RMS) values under the effect of parametric uncertainties and external disturbances, table 2 compares tracking errors for various control strategies. The proposed control scheme outperforms SWTC, PI, and QFT controllers in terms of tracking errors. Moreover, the proposed control scheme is shown to be robust under a wide range of uncertainties (±5% to ±15%) and external disturbances. Additionally, the response of power versus varying wind speed has been plotted for VSWT using the proposed controller and compared with SWTC, PI, and QFT controllers.
The responses shown in figure 12 demonstrate that the proposed controller achieves a higher maximum power compared to other controllers. Therefore, it can be concluded that the proposed control method provides greater power capacity than the existing controllers and also exhibits robust performance overall.
To demonstrate the effectiveness of the proposed bounded UDE-based controller (33), its performance is analyzed in situations where the controller output remains within the specified bounds. The results confirm that it achieves behavior similar to the conventional UDE controller (22). Both the bounded and conventional UDE controllers are compared using the same parameter settings. Furthermore, any reduction in 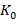 can be compensated by appropriately designing
can be compensated by appropriately designing 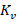 in the controller.
in the controller.
This paper presents a comprehensive VSWT model incorporating aerodynamics, parametric uncertainties, external disturbances, and tower dynamics to realistically capture wind turbine behavior. A BUE-based robust controller is developed to effectively handle uncertainties and varying wind conditions, resulting in improved power generation, rotor speed regulation, and reduced control effort. Simulation study demonstrates satisfactory results in terms of uncertainty estimation and enhanced control performance, leading to increased power output. The proposed controller successfully maximizes power extraction in region tracking control (in TCR) and maintains stable rated power in rated power control (in PCR), highlighting its potential for practical VSWT applications. While the results are promising, future work may focus on advanced uncertainty estimation methods, machine learning-based adaptive control, and validation under wider operating conditions.
|
Symbols |
Parameters |
Values |
|
|
Air density |
|
|
|
Nominal power output |
|
|
|
Gear box ratio |
97 |
|
|
Optimal angular velocities of the rotor |
|
|
|
Nominal angular velocity of the generator |
|
|
|
Minimum angular velocity of the generator |
|
|
|
Moment of inertia (rotor side) |
|
|
|
Moment of inertia (generator side) |
|
|
|
Spring constant |
|
|
|
Damping coefficient |
|
|
|
Radius of blade |
|
|
|
Height of the tower |
|
|
|
Mass constant of the tower |
|
|
|
Spring constant |
|
|
|
Damping constant |
|
|
|
Natural frequency of the actuator |
|
|
|
Damping of pitch actuator |
0.9 |
|
|
Time constant |
|
|
|
Reference generator torque |
|
|
|
Reference pitch angle |
|
|
|
Performance coefficient |
--- |
|
|
Maximum performance coefficient |
--- |
|
|
Speed of wind |
--- |
|
|
Relative wind speed |
--- |
|
|
Tip speed ratio |
--- |
|
|
Optimal tip speed ratio |
--- |
|
|
Thrust force |
--- |
|
|
Coefficient of thrust |
--- |
|
|
Twist |
--- |
|
|
Generator torque |
--- |
|
|
Displacement of the nacelle |
--- |
|
|
Velocity of the tower |
--- |
|
|
Angular velocity of the rotor |
--- |
|
|
Rated angular velocities of rotor |
--- |
|
|
Angular velocities of the generator |
--- |
|
|
Pitch angle of the blade |
--- |
|
|
Optimal pitch angle |
--- |
|
|
Power output |
--- |
1 A.S. Jaber, H.B. Mahdi, T.A. Abdul-Jabbar, H. Kotb, K.M. AboRas, Y.Y. Ghadi, A. Emara, A. Oubelaid, Wind Engineering 48(5) (2024) 954. https://doi.org/10.1177/0309524X241230632
2 J. Wang, F. Golnary, S. Li, A.U. Weerasuriya, K.-T. Tse, Ocean Engineering 311 (2024) 118806. https://doi.org/10.1016/j.oceaneng.2024.118806
3 N.J. Abbas, D.S. Zalkind, L.Y. Pao, A. Wright, Wind Energy Science 7(1) (2022) 53. https://doi.org/10.5194/wes-7-53-2022
4 V. Rezaei, Active Robust Control of Wind Turbines, M.S. Thesis, Tampere University of Technology, Finland (2014). https://doi.org/10.13140/RG.2.2.13809.28005
5 J. Xie, H. Dong, X. Zhao, Renewable Energy 215 (2023) 118893. https://doi.org/10.1016/j.renene.2023.06.014
6 B. Torchani, A.T. Azar, S. Ahmed, A.R. Mahlous, I.K. Ibraheem, Frontiers in Energy Research 12 (2024) 1434695. https://doi.org/10.3389/fenrg.2024.1434695
7 T. Li, J. Yang, A. Ioannou, Renewable Energy 234 (2024) 121265. https://doi.org/10.1016/j.renene.2024.121265
8 H. Moradi, G. Vossoughi, Energy 90 (2015) 1508. https://doi.org/10.1016/j.energy.2015.06.100
9 T.V. Vu, I.S. Ahmed, H. Yoo, Engineering Applications of Artificial Intelligence 156 (2025) 111156. https://doi.org/10.1016/j.engappai.2025.111156
10 P. Lu, N. Zhang, L. Ye, E. Du, C. Kang, Advances in Applied Energy 14 (2024) 100177. https://doi.org/10.1016/j.adapen.2024.100177
11 K. Stol, Disturbance Tracking and Blade Load Control of Wind Turbines in Variable Speed Operation, National Renewable Energy Laboratory (NREL), Golden, CO, USA, NREL/CP-500-33011 (2003). https://doi.org/10.1115/WIND2003-1042
12 S. Rajendran, D. Jena, Journal of Wind Energy 2014 (2014) 1. https://doi.org/10.1155/2014/709128
13 K. Johnson, L. Pao, M. Balas, L. Fingersh, IEEE Control Systems Magazine 26(3) (2006) 70. https://doi.org/10.1109/MCS.2006.1636314
14 A. Jain, G. Schildbach, L. Fagiano, M. Morari, Renewable Energy 80 (2015) 664. https://doi.org/10.1016/j.renene.2015.02.057
15 N. Singh, B. Pratap, A. Swarup, in: Proceedings of the 4th IFAC Conference on Advances in Control and Optimization of Dynamical Systems, Tiruchirappalli, India (2016) 718.
16 A. Kumar, K. Stol, Wind Energy 13(5) (2010) 419. https://doi.org/10.1002/we.363
17 M. Abolvafaei, S. Ganjefar, European Journal of Control 60 (2021) 78. https://doi.org/10.1016/j.ejcon.2021.03.008
18 X. Jiao, G. Wang, X. Wang, Z. Zhang, Y. Tian, X. Fan, Journal of Marine Science and Engineering 12(3) (2024) 473. https://doi.org/10.3390/jmse12030473
19 B. Ren, Q.-C. Zhong, J. Chen, IEEE Transactions on Industrial Electronics 62(9) (2015) 5881. https://doi.org/10.1109/TIE.2015.2421884
20 A.K. Pandey, B. Pratap, A. Swarup, International Journal of Energy and Environmental Engineering 13 (2022) 1163. https://doi.org/10.1007/s40095-022-00478-5
21 H. Geng, G. Yang, IEEE Transactions on Energy Conversion 25(2) (2010) 494. https://doi.org/10.1109/TEC.2009.2034366
22 N. Singh, B. Pratap, A. Swarup, 14th IEEE India Council International Conference (INDICON), Roorkee, India (2017) 582p.
23 N. Singh, B. Pratap, A. Swarup, Proceedings of the IMechE, Part A: Journal of Power and Energy 232(6) (2018) 691. https://doi.org/10.1177/0957650917751463
24 S. Frost, S. Balas, A. Wright, Mechatronics 21(4) (2011) 660. https://doi.org/10.1016/j.mechatronics.2011.01.006
25 M. Balas, K. Magar, S. Frost, American Control Conference (ACC), USA (2013) 2220. https://doi.org/10.1109/ACC.2013.6580165
26 B. Boukhezzar, H. Siguerdidjane, M. Hand, Journal of Solar Energy Engineering 128(4) (2006) 516.
27 N. Singh, B. Pratap, A. Swarup, Journal of Engineering Research 7(3) (2019) 258.
28 Y. Wang, B. Ren, Q.-C. Zhong, IEEE Transactions on Industrial Electronics 68(2) (2021) 5881. https://doi.org/10.1109/TIE.2020.2969069
29 P. Asaah, L. Hao, J. Ji, Journal of Modern Power Systems and Clean Energy 9(2) (2021) 367. https://doi.org/10.35833/MPCE.2019.000087
30 J. Rinker, K.L. Dykes, WindPACT Reference Wind Turbines, National Renewable Energy Laboratory (NREL), Golden, CO, USA, NREL/TP-5000-67667 (2018). https://doi.org/10.2172/1432194
31 W. Musial, P. Beiter, J. Nunemaker, D. Heimiller, J. Ahmann, J. Busch, Oregon Offshore Wind Site Feasibility and Cost Study, National Renewable Energy Laboratory (NREL), Golden, CO, USA, NREL/TP-5000-74597 (2019). https://doi.org/10.2172/1570430
A.K. Pandey, B. Pratap, Development of bounded uncertainty estimator based robust control scheme for enhanced performance of variable speed wind turbine using particle swarm optimization, UNEC J. Eng. Appl. Sci. 5(2) (2025) 27-44. https://doi.org/10.61640/ujeas.2025.1203
Anyone you share the following link with will be able to read this content:

This article is licensed under the Creative Commons Attribution ( CC BY 4.0 ) License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
A.S. Jaber, H.B. Mahdi, T.A. Abdul-Jabbar, H. Kotb, K.M. AboRas, Y.Y. Ghadi, A. Emara, A. Oubelaid, Wind Engineering 48(5) (2024) 954. https://doi.org/10.1177/0309524X241230632
J. Wang, F. Golnary, S. Li, A.U. Weerasuriya, K.-T. Tse, Ocean Engineering 311 (2024) 118806. https://doi.org/10.1016/j.oceaneng.2024.118806
N.J. Abbas, D.S. Zalkind, L.Y. Pao, A. Wright, Wind Energy Science 7(1) (2022) 53. https://doi.org/10.5194/wes-7-53-2022
V. Rezaei, Active Robust Control of Wind Turbines, M.S. Thesis, Tampere University of Technology, Finland (2014). https://doi.org/10.13140/RG.2.2.13809.28005
J. Xie, H. Dong, X. Zhao, Renewable Energy 215 (2023) 118893. https://doi.org/10.1016/j.renene.2023.06.014
B. Torchani, A.T. Azar, S. Ahmed, A.R. Mahlous, I.K. Ibraheem, Frontiers in Energy Research 12 (2024) 1434695. https://doi.org/10.3389/fenrg.2024.1434695
T. Li, J. Yang, A. Ioannou, Renewable Energy 234 (2024) 121265. https://doi.org/10.1016/j.renene.2024.121265
H. Moradi, G. Vossoughi, Energy 90 (2015) 1508. https://doi.org/10.1016/j.energy.2015.06.100
T.V. Vu, I.S. Ahmed, H. Yoo, Engineering Applications of Artificial Intelligence 156 (2025) 111156. https://doi.org/10.1016/j.engappai.2025.111156
P. Lu, N. Zhang, L. Ye, E. Du, C. Kang, Advances in Applied Energy 14 (2024) 100177. https://doi.org/10.1016/j.adapen.2024.100177
K. Stol, Disturbance Tracking and Blade Load Control of Wind Turbines in Variable Speed Operation, National Renewable Energy Laboratory (NREL), Golden, CO, USA, NREL/CP-500-33011 (2003). https://doi.org/10.1115/WIND2003-1042
S. Rajendran, D. Jena, Journal of Wind Energy 2014 (2014) 1. https://doi.org/10.1155/2014/709128
K. Johnson, L. Pao, M. Balas, L. Fingersh, IEEE Control Systems Magazine 26(3) (2006) 70. https://doi.org/10.1109/MCS.2006.1636314
A. Jain, G. Schildbach, L. Fagiano, M. Morari, Renewable Energy 80 (2015) 664. https://doi.org/10.1016/j.renene.2015.02.057
N. Singh, B. Pratap, A. Swarup, in: Proceedings of the 4th IFAC Conference on Advances in Control and Optimization of Dynamical Systems, Tiruchirappalli, India (2016) 718.
A. Kumar, K. Stol, Wind Energy 13(5) (2010) 419. https://doi.org/10.1002/we.363
M. Abolvafaei, S. Ganjefar, European Journal of Control 60 (2021) 78. https://doi.org/10.1016/j.ejcon.2021.03.008
X. Jiao, G. Wang, X. Wang, Z. Zhang, Y. Tian, X. Fan, Journal of Marine Science and Engineering 12(3) (2024) 473. https://doi.org/10.3390/jmse12030473
B. Ren, Q.-C. Zhong, J. Chen, IEEE Transactions on Industrial Electronics 62(9) (2015) 5881. https://doi.org/10.1109/TIE.2015.2421884
A.K. Pandey, B. Pratap, A. Swarup, International Journal of Energy and Environmental Engineering 13 (2022) 1163. https://doi.org/10.1007/s40095-022-00478-5
H. Geng, G. Yang, IEEE Transactions on Energy Conversion 25(2) (2010) 494. https://doi.org/10.1109/TEC.2009.2034366
N. Singh, B. Pratap, A. Swarup, 14th IEEE India Council International Conference (INDICON), Roorkee, India (2017) 582p.
N. Singh, B. Pratap, A. Swarup, Proceedings of the IMechE, Part A: Journal of Power and Energy 232(6) (2018) 691. https://doi.org/10.1177/0957650917751463
S. Frost, S. Balas, A. Wright, Mechatronics 21(4) (2011) 660. https://doi.org/10.1016/j.mechatronics.2011.01.006
M. Balas, K. Magar, S. Frost, American Control Conference (ACC), USA (2013) 2220. https://doi.org/10.1109/ACC.2013.6580165
B. Boukhezzar, H. Siguerdidjane, M. Hand, Journal of Solar Energy Engineering 128(4) (2006) 516.
N. Singh, B. Pratap, A. Swarup, Journal of Engineering Research 7(3) (2019) 258.
Y. Wang, B. Ren, Q.-C. Zhong, IEEE Transactions on Industrial Electronics 68(2) (2021) 5881. https://doi.org/10.1109/TIE.2020.2969069
P. Asaah, L. Hao, J. Ji, Journal of Modern Power Systems and Clean Energy 9(2) (2021) 367. https://doi.org/10.35833/MPCE.2019.000087
J. Rinker, K.L. Dykes, WindPACT Reference Wind Turbines, National Renewable Energy Laboratory (NREL), Golden, CO, USA, NREL/TP-5000-67667 (2018). https://doi.org/10.2172/1432194
W. Musial, P. Beiter, J. Nunemaker, D. Heimiller, J. Ahmann, J. Busch, Oregon Offshore Wind Site Feasibility and Cost Study, National Renewable Energy Laboratory (NREL), Golden, CO, USA, NREL/TP-5000-74597 (2019). https://doi.org/10.2172/1570430