UNEC Journal of Engineering and Applied Sciences Volume 5, No 1, pages 35-42 (2025) Cite this article, 943 https://doi.org/10.61640/ujeas.2025.0504
In the field of nanotechnology, one of the most popular topics for current research and development is polymer-based nanocomposites, and the research area covers a wide range of topics. Polymer-based nanocomposites have recently become a focus of interest for the defense industry and other high-tech industries due to their extraordinary properties, both as carrier elements and intermediate elements. CNTs, one of the components of the nanocomposite, have proven to be an ideal choice as fillers for both structural and functional applications due to their extraordinary properties, such as providing an extraordinary improvement in the properties of the polymer matrix, the main component of the nanocomposite [1-{3]. Nanocomposites have significant advantages over traditional materials, such as very high tensile and flexural strength, light weight, high elasticity modulus and wear resistance, high thermal stability, flame retardant properties, improved specific strength and hardness, improved fracture toughness, thermal shock resistance and significant electrical conductivity. These advantages enable the use of nanocomposites in sandwich structures as well as in different structural systems [4-5]. The first study on the stability of functionally graded nanocomposite structural elements was related to single-layer plates and was proposed in the study of Shen [6]. After this study, many research on the stability of single-layer functionally graded nanocomposite structural elements in different conditions [7-11].
One of the most economical ways to obtain satisfactory mechanical properties of structural elements is to perform hybridizations involving the use of more than one composite material. One type of hybrid composites is sandwich structures, which consist of two relatively rigid face layers and a soft core [12].
The most important disadvantage of sandwich structural elements consisting of traditional composites is the delamination of the layers due to the difference in mechanical properties. The discovery of new generation composites plays an important role in eliminating these negativities. In recent years, nanocomposite layers have begun to be frequently used in sandwich systems in various areas of modern technology. In terms of the reliability of these applications, there is a need to investigate the buckling behavior of triple systems containing nanocomposite layers, especially triple-layer plate systems. The number of publications on the buckling problem of sandwich or multi-layer nanocomposite plates is quite limited. Lei et al. [13] studied the buckling behavior of functionally graded layered composite plates reinforced with carbon nanotubes was investigated using the meshless kp-Ritz method. Long and Tung [14] investigated the buckling and post-buckling behavior of sandwich plates reinforced with single-walled carbon nanotubes resting on elastic foundations and subjected to uniform temperature increase. Tan et al. [15] proposed novel sandwich composite shell structures in nonlinear geometric and dynamic analyses. Sofiyev and Avey [16] presented modeling and applications of laminated nanocomposite structural elements in thermal environments. Sofiyev et al. [17] proposed a mathematical approach to the buckling problem of axially loaded laminated nanocomposite cylindrical shells in various environments.
The literature review shows that the buckling behavior of sandwich plates consisting of nanocomposites under the effect of in-plane uniaxial and biaxial compressive forces has not been investigated in detail. Since accurate and effective buckling analysis of sandwich plates containing nanocomposite layers is of critical importance to achieve optimized and reliable designs, this issue will be discussed in detail in this study.
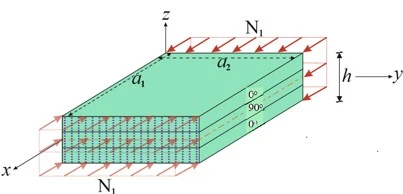
Figure 1. A sandwich rectangular plate containing three nanocomposite layers under uniaxial compressive load and the coordinate system
A sandwich rectangular plate with (0o/90o/0o) arrangement containing nanocomposite layers presented in figure 1 that is under unidirectional compressive load, the length and width are 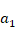 and
and 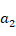 , the thickness of each layer is
, the thickness of each layer is 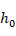 and the total thickness of the sandwich plate is
and the total thickness of the sandwich plate is 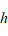 . The compressive load
. The compressive load 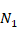 acts in the direction of the
acts in the direction of the 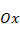 axis. It is assumed that the layers are perfectly and rigidly bonded to each other and that the layers do not break apart when a deformation occurs. The rectangular sandwich plate has a continuous heterogeneous orthotropic structure with pieces, each layer consists of a carbon nanotube reinforced polymer matrix and has the same carbon nanotube volume fraction. The
axis. It is assumed that the layers are perfectly and rigidly bonded to each other and that the layers do not break apart when a deformation occurs. The rectangular sandwich plate has a continuous heterogeneous orthotropic structure with pieces, each layer consists of a carbon nanotube reinforced polymer matrix and has the same carbon nanotube volume fraction. The 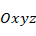 coordinate system is in the back left corner of the origin rectangular sandwich plate and in the reference plane of the middle layer, the
coordinate system is in the back left corner of the origin rectangular sandwich plate and in the reference plane of the middle layer, the 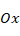 axis is in the longitudinal direction, the
axis is in the longitudinal direction, the 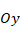 axis is in the transverse direction and the
axis is in the transverse direction and the 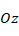 axis is perpendicular to the reference plane. The three perpendicular displacements of any point in the reference plane of the three-layer rectangular plate are shown as U, V and W, respectively.
axis is perpendicular to the reference plane. The three perpendicular displacements of any point in the reference plane of the three-layer rectangular plate are shown as U, V and W, respectively.
In this study, multi-scale modeling of CNTs and polymer matrix is performed. It is known that the effective material properties of nanocomposites largely depend on the structure of CNTs [2-5]. It is well known that to estimate the effective material properties of multilayered and specially sandwich nanocomposite rectangular plates layers, the extended Voigt model is used [6-11], where the CNT efficiency parameters are defined to take into account the size dependence of the resulting nanostructures. According to this rule, the effective Young's modulus and shear modulus of each nanocomposite layer can be estimated as follows [13, 17]:
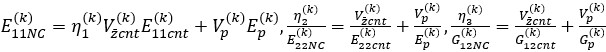 (1)
(1)
where 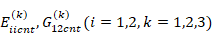 and
and 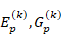 are the Young and shear modulus of elasticity of the k-th layer CNT and polymer, respectively, of the sandwich rectangular plate.
are the Young and shear modulus of elasticity of the k-th layer CNT and polymer, respectively, of the sandwich rectangular plate. 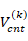 and
and 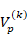 represent the volume fractions of the k-th layer CNT and the polymer matrix, respectively, and the following relation satisfied:
represent the volume fractions of the k-th layer CNT and the polymer matrix, respectively, and the following relation satisfied: 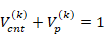 .
.
To account for the small-scale effect, the efficiency parameters of the CN, denoted by 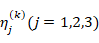 , are obtained by matching the Young moduli of the nanocomposite layer estimated from the extended Voight models with the values found from the molecular dynamics simulations, as previously presented in [3].
, are obtained by matching the Young moduli of the nanocomposite layer estimated from the extended Voight models with the values found from the molecular dynamics simulations, as previously presented in [3].
Since the Poisson's ratio and mass density of the nanocomposite layer vary within a small range, the Poisson's ratio and mass density of the components can be easily expressed according to the traditional mixing rule as:
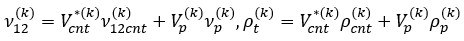 (2)
(2)
The mathematical models characterizing the volume fraction distributions of the k-th layer CNT are given as follows [6, 13, 16]:
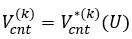 (3)
(3)
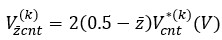 (4)
(4)
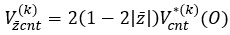 (5)
(5)
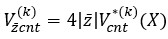 (6)
(6)
Pre-buckling properties of sandwich HT-nanocomposite rectangular plates presented in figure 1 can be expressed as follows and indicated by superscript "0" [18, 19]:
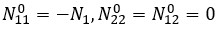 (7)
(7)
where 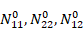 are the membrane forces for the zero initial moment condition.
are the membrane forces for the zero initial moment condition.
The dependence between the 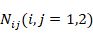 force components and the Airy stress function (
force components and the Airy stress function (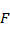 ) is defined as follows [18, 19]:
) is defined as follows [18, 19]:
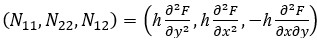 (8)
(8)
Within the framework of classical plate theory, the stress-strain relationships in each layer of sandwich rectangular plates consisting of heterogeneous nanocomposite layers are defined as follows [11, 16]:
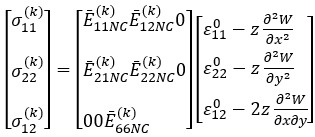 (9)
(9)
where, 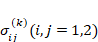 are the stress components in the kth layer,
are the stress components in the kth layer,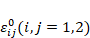 are the strain components in the mid-plane of the three-layer rectangular plate consisting of nanocomposite layers and
are the strain components in the mid-plane of the three-layer rectangular plate consisting of nanocomposite layers and 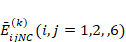 are the coefficients defining the elastic properties of the layers consisting of nanocomposites are expressed as follows:
are the coefficients defining the elastic properties of the layers consisting of nanocomposites are expressed as follows:
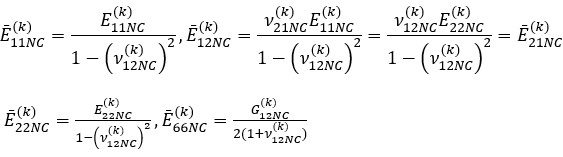 (10)
(10)
The forces and moments are defined as follows [18, 19]:
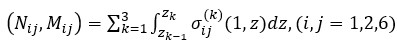 (11)
(11)
where
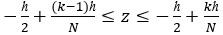 (12)
(12)
By using the relationships from (9) to (11), the governing equations for sandwich heterogeneous plates composed within CPT are obtained as follows:
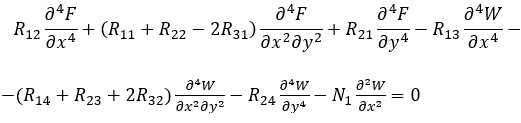 (13)
(13)
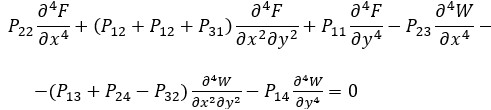 (14)
(14)
where 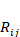 and
and 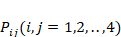 denote parameters depending on the elastic properties of sandwich plates consisting of FG-nanocomposite layers.
denote parameters depending on the elastic properties of sandwich plates consisting of FG-nanocomposite layers.
Since all edges of the sandwich plate are assumed to be simply supported, the solution of (13) and (14) is sought as follows [18, 19]:
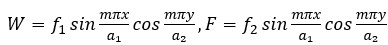 (15)
(15)
where 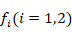 denote unknown amplitudes,
denote unknown amplitudes, 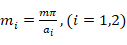 denote the wave parameters in which (m, n) is the wave mode.
denote the wave parameters in which (m, n) is the wave mode.
Substituting (15) into the set of equations (14) and (13), then using Galerkin procedure and eliminating the unknown 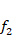 from the resulting equations and is considered
from the resulting equations and is considered 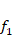 to be nonzero, we obtain following expression for the dimensionless critical uniaxial compressive load sandwich plates consisting of the nanocomposite layers,
to be nonzero, we obtain following expression for the dimensionless critical uniaxial compressive load sandwich plates consisting of the nanocomposite layers,
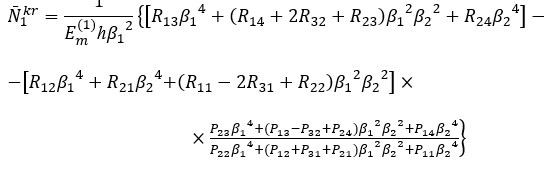 (16)
(16)
In this subsection, the dimensionless uniaxial critical load values of sandwich plates consisting of homogeneous and heterogeneous nanocomposite layers with CNT welded (0o/90o/0o) and (90o/0o/90o) alignments are analyzed in comparison with single-layered plates with (0o) alignment. The properties of the nanocomposite consisting of single-walled CNT reinforced polymethyl methacrylate (PMMA) forming the layers of the sandwich plates are presented in table 1. Those data are taken from the study of Shen [7].
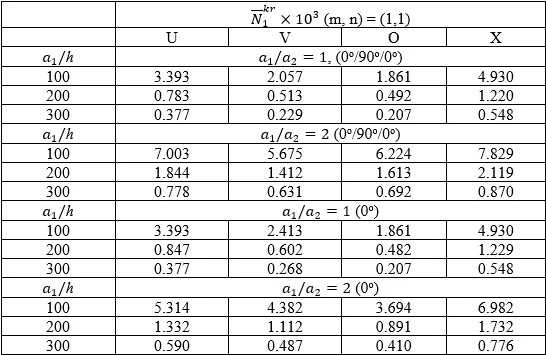
Table 2. Distributions of  for (0o) single-layer and (0º/90º/0º) sandwich nanocomposite plates versus the
for (0o) single-layer and (0º/90º/0º) sandwich nanocomposite plates versus the  ratio for different
ratio for different 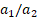
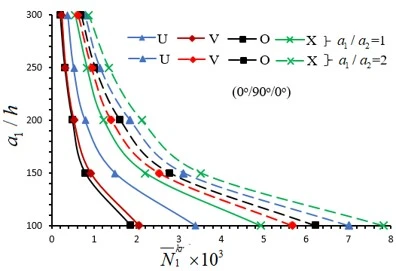
Figure 2. Distribution of dimensionless critical load values of sandwich plate with U, V, O and X pattern (0o/90o/0o) arrangement versus 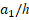 for different
for different 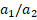
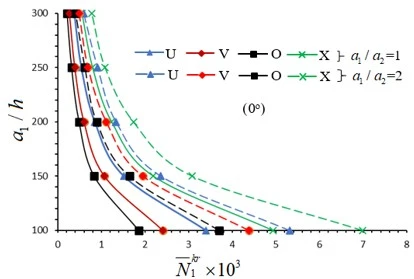
Figure 3. Distribution of dimensionless critical load values of (0o) single-layer plate with U, V, O and X patterns versus the 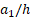 for different
for different 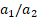
The distributions of the values of 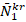 for U, V, O and X patterned (0o) single-layer and sandwich nanocomposite plates with (0°/90°/0°) alignment subjected to compressive uniaxial load in the Ox direction depending on the
for U, V, O and X patterned (0o) single-layer and sandwich nanocomposite plates with (0°/90°/0°) alignment subjected to compressive uniaxial load in the Ox direction depending on the 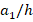 for 1
for 1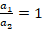 and 2 are presented in table 2 and figures 2 and 3. As can be seen from table 2, when the
and 2 are presented in table 2 and figures 2 and 3. As can be seen from table 2, when the 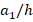 ratio increases, the critical load values decrease in all patterns of sandwich plates with (0o/90o/0o) alignment and (0o) single-layer plates, while the values of the wave number remain constant. As can be seen from table 2 and figures 2 and 3, as the dimensionless critical compressive load values of the (0o/90o/0o) arrangement sandwich plates with V, O and X patterns are compared with the dimensionless critical load values of the U patterned plate, the influences of V, O and X patterns change irregularly as the
ratio increases, the critical load values decrease in all patterns of sandwich plates with (0o/90o/0o) alignment and (0o) single-layer plates, while the values of the wave number remain constant. As can be seen from table 2 and figures 2 and 3, as the dimensionless critical compressive load values of the (0o/90o/0o) arrangement sandwich plates with V, O and X patterns are compared with the dimensionless critical load values of the U patterned plate, the influences of V, O and X patterns change irregularly as the 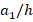 ratio increases. For example, for
ratio increases. For example, for 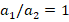 , the influences of V, O and X patterns on the critical load are 39.4%, 45.2% and (-45.3%), respectively, as
, the influences of V, O and X patterns on the critical load are 39.4%, 45.2% and (-45.3%), respectively, as 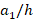 = 100, while those effects are 34.5%, 37.2% and (-55.8%), when
= 100, while those effects are 34.5%, 37.2% and (-55.8%), when 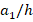 = 200 and 39.3%, 45.1% and (-45.2%), respectively, when
= 200 and 39.3%, 45.1% and (-45.2%), respectively, when 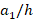 = 300. At
= 300. At 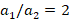 , the influences of V, O and X patterns on the critical load are 19%, 11.1%, and (-11.8%), respectively, as
, the influences of V, O and X patterns on the critical load are 19%, 11.1%, and (-11.8%), respectively, as 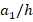 = 100, while those effects are 23.4%, 12.5% and (-14.9%), when
= 100, while those effects are 23.4%, 12.5% and (-14.9%), when 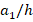 = 200 and 18.9%, 11.1% and (-11.8%), respectively, when
= 200 and 18.9%, 11.1% and (-11.8%), respectively, when 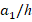 = 300. When the critical load values of V, O and X patterned plates with (0o/90o/0o) alignment are compared with the critical load values of the U patterned plate with (0o/90o/0o) alignment, it is seen that the largest effect is in the X pattern and the smallest effect is in the O pattern.
= 300. When the critical load values of V, O and X patterned plates with (0o/90o/0o) alignment are compared with the critical load values of the U patterned plate with (0o/90o/0o) alignment, it is seen that the largest effect is in the X pattern and the smallest effect is in the O pattern.
When the critical load values of (0°/90°/0°) arranged V, O and X patterned plates are compared with the critical load values of (0o) arranged patterned plates, when 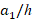 =100, the ratio difference between the critical load values is 10.49%, 0% and 0%, respectively. Those effects do not change in O and X, but decrease in V the pattern. It is seen that V, O, and X patterns are 10.35%, 0% and 0%, respectively. Therefore, sandwich plates reduce the critical load values compared to (0o) single layer plates.
=100, the ratio difference between the critical load values is 10.49%, 0% and 0%, respectively. Those effects do not change in O and X, but decrease in V the pattern. It is seen that V, O, and X patterns are 10.35%, 0% and 0%, respectively. Therefore, sandwich plates reduce the critical load values compared to (0o) single layer plates.
In this study, the buckling of polymer-based sandwich rectangular plates with uniform and heterogeneous nanocomposite layers of CNT reinforcement subjected to uniaxial compressive loads is investigated. After construction of governing relations of sandwich plates consisting of polymer-based nanocomposite layers, the stability and strain compatibility equations are derived based on the assumptions of classical plate theory. Analytical expressions for the uniaxial critical compressive load are found for simply supported boundary conditions. Finally numerical calculations are made for the minimum values of the uniaxial critical compressive load for four different CNT patterns in the layers and various plate sizes and those calculations are interpreted.
1 S. Iijima, Nature 354 (1991) 56. http://dx.doi.org/10.1038/354056a0
2 P. Ajayan, L. Schadler, P. Braun, Nanocomposite science and technology. Wiley‐VCH Verlag GmbH & Co. KGaA (2003). http://dx.doi.org/10.1002/3527602127
3 Y. Han, J. Elliott, Computational Materials Science 39 (2007) 315. https://doi.org/10.1016/j.commatsci.2006.06.011
4 M. Kessler, W. Goertzen, Nanotechnology in Construction 3 (2009) 241. https://doi.org/10.1007/978-3-642-00980-8_32
5 K.M. Liew, Z.H. Pan, L.W. Zhang, Science China-Physics, Mechanics & Astronomy 63(3) (2020) 234601. https://ui.adsabs.harvard.edu/link_gateway/2020SCPMA..6334601L/doi:10.1007/s11433-019-1457-2
6 6. H-S. Shen, Composite Structures 91(1) (2009) 9. http://dx.doi.org/10.1016/j.compstruct.2009.04.026
7 H.-S. Shen, C.L. Zhang, Materials and Design 31(7) (2010) 3403. http://dx.doi.org/10.1016/j.matdes.2010.01.048
8 M. Mirzaei, Y. Kiani, Meccanica 51(9) (2016) 2185. http://dx.doi.org/10.1007/s11012-015-0348-0
9 A. Farzam, B. Hassani, Composite Structures 206 (2018) 774. https://doi.org/10.1016/j.compstruct.2018.08.030
10 A. Sofiyev, U. Kaya, UNEC Journal of Engineering and Applied Sciences 2(1) (2022) 19.
11 M. Avey, N. Fantuzi, A.H. Sofiyev, Mathematics 10(7) (2022) 1081. https://doi.org/10.3390/math10071081
12 D. Zenkert, An introduction to sandwich construction; Engineering materials advisory services (EMAS): London, UK; Stockholm, Sweden (1995).
13 Z.X. Lei, L.W. Zhang, K.M. Liew, Composite Structures 152 (2016) 62. https://doi.org/10.1016/j.compstruct.2016.05.047
14 V.T. Long, H.V. Tung, Journal of Thermal Stresses 42(5) (2019) 658. http://dx.doi.org/10.1177/0892705719828789
15 N. C. Tan, N. M. Dzung, N. H. Ha, N. D.Tien, N. C. Hung, A. H. Sofiyev, D. G. Ninh AIAA Journal 1 (2025) 1. https://doi.org/10.2514/1.J065315
16 A.H. Sofiyev, M. Avey, Mathematical Methods in the Applied Sciences 9999 (2025) 1. http://dx.doi.org/10.1002/mma.10820
17 A.H. Sofiyev, M. Avey, N.M. Aslanova, Mathematical and Computational Applications 30 (1) (2025) 1. https://doi.org/10.3390/mca30010010
18 M.R. Eslami, Buckling and postbuckling of beams, plates and shells. Springer, Switzerland (2018) 603 p.
19 J.N. Reddy, Mechanics of laminated composite plates and shells: theory and analysis. 2nd ed. CRC Press, New-York (2004) 858 p. https://doi.org/10.1201/b12409
C. Bozkurt, H. Dilmac, A.H. Sofiyev, Buckling problem of sandwich rectangular plates consisting of polymer-based nanocomposite layers under compressive load, UNEC J. Eng. Appl. Sci. 5(1) (2025) 35-42. https://doi.org/10.61640/ujeas.2025.0504
Anyone you share the following link with will be able to read this content:
S. Iijima, Nature 354 (1991) 56. http://dx.doi.org/10.1038/354056a0
P. Ajayan, L. Schadler, P. Braun, Nanocomposite science and technology. Wiley‐VCH Verlag GmbH & Co. KGaA (2003). http://dx.doi.org/10.1002/3527602127
Y. Han, J. Elliott, Computational Materials Science 39 (2007) 315. https://doi.org/10.1016/j.commatsci.2006.06.011
M. Kessler, W. Goertzen, Nanotechnology in Construction 3 (2009) 241. https://doi.org/10.1007/978-3-642-00980-8_32
K.M. Liew, Z.H. Pan, L.W. Zhang, Science China-Physics, Mechanics & Astronomy 63(3) (2020) 234601. https://ui.adsabs.harvard.edu/link_gateway/2020SCPMA..6334601L/doi:10.1007/s11433-019-1457-2
6. H-S. Shen, Composite Structures 91(1) (2009) 9. http://dx.doi.org/10.1016/j.compstruct.2009.04.026
H.-S. Shen, C.L. Zhang, Materials and Design 31(7) (2010) 3403. http://dx.doi.org/10.1016/j.matdes.2010.01.048
M. Mirzaei, Y. Kiani, Meccanica 51(9) (2016) 2185. http://dx.doi.org/10.1007/s11012-015-0348-0
A. Farzam, B. Hassani, Composite Structures 206 (2018) 774. https://doi.org/10.1016/j.compstruct.2018.08.030
A. Sofiyev, U. Kaya, UNEC Journal of Engineering and Applied Sciences 2(1) (2022) 19.
M. Avey, N. Fantuzi, A.H. Sofiyev, Mathematics 10(7) (2022) 1081. https://doi.org/10.3390/math10071081
D. Zenkert, An introduction to sandwich construction; Engineering materials advisory services (EMAS): London, UK; Stockholm, Sweden (1995).
Z.X. Lei, L.W. Zhang, K.M. Liew, Composite Structures 152 (2016) 62. https://doi.org/10.1016/j.compstruct.2016.05.047
V.T. Long, H.V. Tung, Journal of Thermal Stresses 42(5) (2019) 658. http://dx.doi.org/10.1177/0892705719828789
N. C. Tan, N. M. Dzung, N. H. Ha, N. D.Tien, N. C. Hung, A. H. Sofiyev, D. G. Ninh AIAA Journal 1 (2025) 1. https://doi.org/10.2514/1.J065315
A.H. Sofiyev, M. Avey, Mathematical Methods in the Applied Sciences 9999 (2025) 1. http://dx.doi.org/10.1002/mma.10820
A.H. Sofiyev, M. Avey, N.M. Aslanova, Mathematical and Computational Applications 30 (1) (2025) 1. https://doi.org/10.3390/mca30010010
M.R. Eslami, Buckling and postbuckling of beams, plates and shells. Springer, Switzerland (2018) 603 p.
J.N. Reddy, Mechanics of laminated composite plates and shells: theory and analysis. 2nd ed. CRC Press, New-York (2004) 858 p. https://doi.org/10.1201/b12409