Investigation of buckling behavior of functionally graded carbon nanotube patterned polymer plates in thermal environments

Abstract

Introduction

The groundbreaking paper on carbon nanotubes (CNTs) by Iijima in 1991 is considered a major breakthrough in science. This discovery paved the way for the use of CNTs in many applications, with their outstanding mechanical, electrical and thermal properties. CNTs can be classified into two types: single-walled carbon nanotubes (SWCNTs) and multi-walled carbon nanotubes (MWCNTs) [1,2]. It should be emphasized that CNTs with a radius of 1-2 nm have the same elastic properties with a Young's modulus of about 1 TPa and a shear modulus of about 0.45 TPa [3]. Many studies have been conducted on the superior electrical, optical, mechanical and thermal properties of CNTs [4,5]. For decades, fiber reinforcements have been used to achieve high specific strength and stiffness in weight-sensitive structural applications such as composite materials, marine, construction, mechanical, automotive and aircraft structures. However, this reinforcement had some disadvantages as it increased the weight of structural elements. With the discovery of carbon nanotubes, this disadvantage began to disappear. It has been scientifically proven that the discovery of CNT and its reinforcement into the matrix significantly improves the thermal and mechanical properties of the composites [6-9].
These developments have led to the proposition of a new type of CNT-reinforced composite material that has attracted increasing attention [10]. Inspired by the concept of functionally graded materials, CNT reinforced composites are a functionally graded nanocomposite model. CNTs are uniaxially strengthened, aligned in the axial direction, and the material properties are graded in the thickness direction, forming a reinforced FG-CNT composite [11]. The FG-CNT reinforced composites are the advanced composite materials that forms structural components such as beams, plates or shells. The study of the mechanical behavior FG-CNT reinforced composite structural elements have always been the focus of attention of researchers. For example, thermal buckling and post-buckling behavior of FG-CNT reinforced composite plates exposed to in-plane heat is investigated by Shen and Zhang [12]. The same methodology was extended by Shen [13] to study FG-CNT patterned shell problems. The finite element method is used by Zhu et al. [14] to examine the static and free vibration of FG-CNT reinforced composite plates. Free vibration analysis of functionally graded carbon nanotube-reinforced composite plates using the element-free kp-Ritz method in thermal environment is performed in the study of Lei et al. [15]. Static analysis of CNT-reinforced composite rectangular plates bonded to thin piezoelectric layers exposed to thermal load and/or electric fields was performed by Alibeigloo [16]. Zhang et al. [17] used the Ritz method to examine the free vibration of FD-CNT reinforced composite plate problem. Sofiyev et al. [18-20] investigated buckling behaviors of various FG-CNT reinforced structural members under different loading conditions. 
Therefore, it is necessary to examine the buckling problem of rectangular plates which is one of the structural elements composed of FG-CNT patterned polymers, to provide more useful parameters for successful engineering practice. The literature review reveals that the buckling problem of functionally graded carbon nanotube reinforced rectangular plates in thermal environments under compressive load has not been sufficiently studied. In the study, this subject will be discussed in detail.

Formulation of problem

In Figure 1, the selected Oxyz coordinate system is presented on the midplane of the CNT reinforced rectangular plate with side lengths a and b, and thickness h. Here, while the x and y axes are oriented in the longitudinal and transverse directions, the z axis is normal to the xy plane and points inwards. The displacements along the x,y and z axes are denoted by u,v and w respectively. The material properties of the nanocomposite plate are dependent of location (z1=z/h) and temperature (T) and under compressive load in the direction of x-axis.

Figure 1. CNT-reinforced rectangular plate under compressive load and coordinate system

We assume that the material properties of CNTs and polymer are temperature dependent [14]:

(1)

where, the elastic properties of CNT and polymer are denoted by Yijcnt(T), (i,j=1,2) and Ym(T) respectively; ηj(j=1,2,3) represents the productivity parameters for CNTs; Vcntz1 and Vm are the volume fractions of CNTs and polymer, respectively, with Vcntz1+Vm=1, and the following expression is valid for the total volume fraction of CNTs [11]:

                                            (2)

where, mcnt is the mass of CNT, Vcnt* is the fraction of total volume fraction of CNT, ρcnt and ρm are the densities of CNT and polymer and Vcntz1are defined as (see, Figure 2):

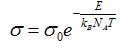                           (3)

The cross-sections of the nanocomposite plate with (a) UD, (b) VD, (c ) OD  and (d) XD profiles are shown in Figure 2.

Figure 2. Cross sections of rectangular plates with CNT profiles (a) UD, (b) VD, (c) OD, (d) XD

Basic equations and solution procedure

In the framework of classical theory, the linear constitutive relations for FG-CNT reinforced plates are defined as follows [6]:

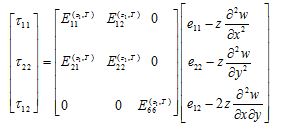                         (4)

where τij(i=1,2) are the stresses, eij(i=1,2) are the strains on the midplane, Eij(z1,T)are the functionally graded material properties of rectangular plates and are defined by,

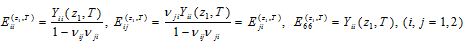 (5)

In the framework of CT the force and moment components of nanocomposite plates are found from the following expressions [19-21]:

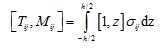                                                            (6)

The matrix form of the relations between the in-plane forces and the Airy stress function F is presented below [21]:

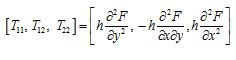                                                                    (7)

Using equations (1),(4),(6) and (7) the linear basis stability and compatibility equations for FG-CNT-reinforced plates are derived as follows:

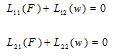                                                                   (8)

where Lij(i,j=1,2) are differential operators and are defined as:

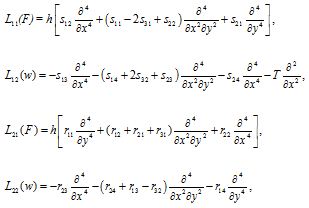                                                        (9)

in which sij and rij (i,j=1,2,3,4) included in these differential operators are the temperature dependent coefficients of rectangular plates with CNT profiles.
For a simply supported nanocomposite rectangular plate reinforced by CNTs, the displacement and Airy stress functions are sought as follows [20,21]:

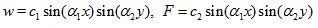                                                      (10)

where ci(i=1,2) are unknown amplitudes, α1=mπa, α2=nπb in which m,n is the buckling mode.

Substituting expressions (10) into the system of equations (8), multiplying the obtained expressions by the weight function, and applying the Galerkin method, the following expression is obtained for the dimensionless critical load for FG-CNT reinforced rectangular plates:

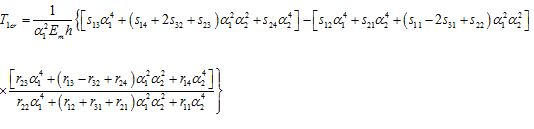  (11)

Results and discussions

In this section, the following materials and data are used to make original numerical analyzes. A poly (methyl methacrylate) called PMMA reinforced with (10,10) single walled CNTs is used. The elastic properties of the PMMA are: Ym=2.5×109Pa, νm=0.34 and  ρm=1.15×103kg/m3. The geometry and elastic properties of CNT are defined as: rcnt=9.26nm,  acnt=0.68nm,  hcnt=0.067nm and Y11cnt=5.6466​×1012Pa, Y22cnt=7.08×1012Pa,  ν12cnt=0.175, ρcnt=1.4×103kg/m3. The temperature-dependent properties of the polymer reinforced with CNT were defined in the work [11] and the same data are used in this study. The total volume fraction and efficiency parameters of CNTs are given in Table 1.

Table 1. The total volume fractions and productivity parameters of CNTs

In Table 2, the distribution of the dimensionless critical load depending on the change of the volume fraction is presented for different temperature. The plate dimensions are taken into account as b=0.3411, a/b=1, h=b/50 in the numerical calculations. As can be seen from Table 2, when volume fraction increases, the values ​​of the dimensionless critical load increment, and the increase of temperature decreases the dimensionless critical load values, albeit weakly. The minimum value of the dimensionless critical load occurs at m,n=1,1. It can be seen from Table 2 that while the dimensionless critical load values of the plate with U profile are higher than the dimensionless critical load values of plates with the O and X profiles, those values are smaller than the dimensionless critical load values of the plate with XD profile.  The effect of functionally graded profiles on the dimensionless critical load differs compared to the uniform profile. It is seen that the greatest effect on the dimensionless critical load occurs in the XD profile, and it has been found that this effect increases depending on the temperature. For example, when T=300 (K), the pattern effects on critical load are 45.29%, 45.52% and 47.7% respectively, while for T=750 (K) those effects are 47.98%, 48.09% and 49.05% for Vcnt*=0.12, 0.17 and 0.28, respectively. When the temperature changes from 300 (K) to 700 (K), the effect difference between the dimensionless critical load values ​​in the XD profile becomes 7.42%, 7.66% and 6.52% for Vcnt*=0.12, 0.17 and 0.28, respectively. Since the dimensionless critical load values ​​of plates with VD and OD profiles are the same, their effects on the buckling behavior of the plate are also the same, and the effect of the VD or OD patterns on the dimensionless critical load is about 29%-30% less than the effects of the XD profile.

Table 2. Distribution of the dimensionless critical load depending on the change of the volume fraction for different temperatures

Conclusion

In this study, the buckling of composite rectangular plates patterned by CNTs under unidirectional compressive loads in the thermal environments is investigated based on the Kirchhoff-Love hypothesis. The governing equations of rectangular plates modeled by CNTs are derived using modified Donnell type plate theory. Then, by applying Galerkin's method, the basic equations are solved and an analytical expression for the dimensionless critical load is obtained. The effects of temperature, volume fraction and nanocomposite profiles on the critical axial load are discussed. The analyzes and comments revealed that the variations of temperature and volume fraction have a significant effect on the dimensionless critical load and these factors should be taken into account during the design of nanocomposite plates in the thermal environments.

References

About this article