UNEC Journal of Engineering and Applied Sciences Volume 5, No 1, pages 63-69 (2025) Cite this article, 430 https://doi.org/10.61640/ujeas.2025.0507
In recent years, the growing demand for high-temperature thermal sensors has advanced the production of Distributed Temperature Sensors into a new stage of development [1-8]. A new type of sensor, combined with a microswitch-based specialized assembly device, offers convenience by integrating all components into a single structure [9-13]. This innovative system features a special heater that activates at the point of data acquisition without influencing the external connection conditions. Additionally, the diode temperature sensor (DTS), positioned some distance from the heater, enables the measurement of pressure, humidity, and mass flow by monitoring temperature [9,14-16]. Since these sensors are primarily derived from silicon structures, it is essential to understand the maximum operating range of silicon-based DTSs.
The relevance of this work lies in determining the maximum temperature range of silicon diode temperature sensors when operating at high temperatures, as well as developing the limiting characteristics that define measurement accuracy. The aim of this research is to enhance the performance efficiency of silicon diode thermal sensors and to expand their potential applications in new conditions.
In this section, we propose criteria for determining the maximum operating temperature and measurement errors of silicon-based DTS when identifying their limiting characteristics.
To achieve this, we use the following model to determine the limiting characteristics of silicon DTS:
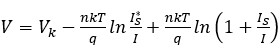 (1)
(1)
where 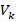 is the built-in potential [
is the built-in potential [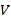 ],
], 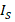 and
and 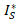 are the saturation currents for reverse and forward connections [
are the saturation currents for reverse and forward connections [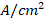 ], respectively,
], respectively, 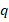 is the charge of an electron [C],
is the charge of an electron [C], 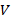 is the voltage across the diode (
is the voltage across the diode (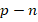 junction) [
junction) [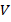 ],
], 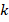 is Boltzmann's constant [
is Boltzmann's constant [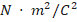 ],
], 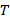 is the temperature [
is the temperature [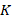 ], and,
], and, 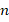 is the non-ideality coefficient.
is the non-ideality coefficient.
The proposed equation 1 consists of three terms, with the second term, 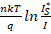 , representing the variation of the saturation current as a function of temperature. Unlike previous studies [1,11,12], we introduce this second term into the existing model. To derive this term, we propose the following expression for
, representing the variation of the saturation current as a function of temperature. Unlike previous studies [1,11,12], we introduce this second term into the existing model. To derive this term, we propose the following expression for 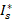 :
:
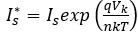 (2)
(2)
where 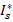 is introduced as a parameter characterizing the variation of the forward saturation current.
is introduced as a parameter characterizing the variation of the forward saturation current.
By incorporating this modification, as previously highlighted, we reformulate Shockley’s equation, introducing a new term into the final equation, resulting in the form given in equation 1. A detailed description of equation 1 can be found in [17,18].
The validation of the proposed model was performed by comparing the analytically calculated voltage-temperature dependence with the experimental results reported in [19–21]. figures 1 and 2 illustrate this comparison.
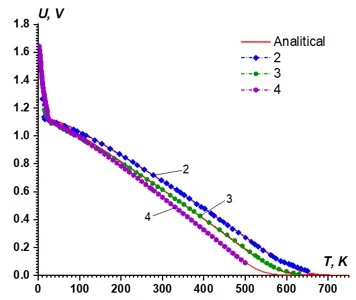
Figure 1. Temperature response curves for silicon diodes: 1 – analytical model (1); experimental data: 2, 3 – [19], 4 – [20]
As observed in figure 1, the analytical calculations closely correspond to the experimental data across almost the entire temperature range. In particular, within the range of 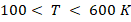 , the model exhibits strong agreement with experimental results. However, some deviations are observed at both high and cryogenic temperatures, which may be attributed to experimental conditions, measurement accuracy, and additional physical processes.
, the model exhibits strong agreement with experimental results. However, some deviations are observed at both high and cryogenic temperatures, which may be attributed to experimental conditions, measurement accuracy, and additional physical processes.
In figure 2, discrepancies between the analytical and experimental results can be seen, which may be explained by variations in the current transport mechanism, measurement uncertainties, and systematic errors. Nevertheless, it is important to emphasize that the proposed analytical model is applicable only in cases where the diffusion mechanism dominates the current transport process.
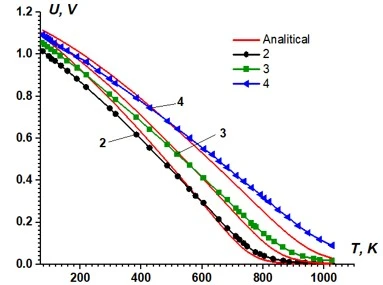
Figure 2. Temperature response curves for silicon diodes: 1– analytical model (1); experimental data: 2,3,4 – [21]
The results presented in figures 1 and 2 were also evaluated statistically. The correlation coefficient 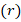 and the coefficient of determination
and the coefficient of determination 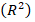 – which characterize the consistency between the analytical and experimental results – were found to be 0.99 and 0.98, respectively. This confirms the high accuracy of the proposed model.
– which characterize the consistency between the analytical and experimental results – were found to be 0.99 and 0.98, respectively. This confirms the high accuracy of the proposed model.
Furthermore, the error analysis yielded root mean square error (RMSE) and mean absolute error (MAE) values of 0.025 V and 0.02 V, respectively, indicating a strong agreement between the model and experimental data.
Overall, the adequacy of the proposed model for real systems has been validated, suggesting its potential application in future sensor design and optimization processes.
Based on this model, we determine the maximum operating temperature and measurement errors of a sensor with a given accuracy using the following criteria:
4.1. Determination of the Maximum Temperature of Silicon Diode Temperature Sensors
The scenarios illustrated in figure 3 include the following:
- Curve 1 represents the complete model graph.
- Curves 2, 3, and 4 correspond to the graphs determined by the first, second, and third terms of equation 1, respectively.
It is well known that temperature sensors operate in a linear region. The point at which the transition to the nonlinear region begins is considered the maximum operating temperature. This transition point occurs when the first and second terms in the model are equal.
From this, by equating the first two terms:
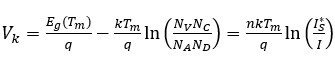 (3)
(3)
We derive a transcendental equation from expression (2) that enables us to determine the maximum temperature 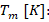
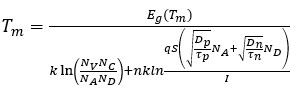 (4)
(4)
where 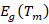 is the bandgap energy [
is the bandgap energy [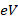 ] at
] at 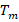 ,
, 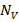 and
and 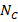 are the effective density of states for holes and electrons [
are the effective density of states for holes and electrons [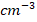 ],
], 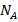 and
and 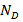 are the acceptor and donor concentrations [
are the acceptor and donor concentrations [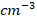 ],
], 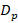 and
and 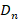 are the diffusion coefficients for holes and electrons [
are the diffusion coefficients for holes and electrons [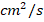 ],
], 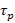 and
and 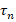 are their lifetimes
are their lifetimes 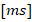 , and
, and 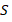 is the heat exchange surface area
is the heat exchange surface area 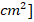 .
.
4.2. Systematic errors during diode operation
a) Errors due to self-heating
The current passing through the 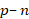 junction generates Joule heat, leading to self-heating of the diode. Consequently, the temperature of the
junction generates Joule heat, leading to self-heating of the diode. Consequently, the temperature of the 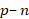 junction will be higher than the semiconductor surface temperature, which exchanges heat with the environment, by a value of
junction will be higher than the semiconductor surface temperature, which exchanges heat with the environment, by a value of 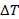
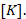 Therefore, the maximum operating current of the diode is limited by its self-heating process, and the resulting
Therefore, the maximum operating current of the diode is limited by its self-heating process, and the resulting 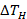 error [
error [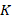 ] must not exceed the measurement error
] must not exceed the measurement error 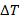 . This is defined as:
. This is defined as:
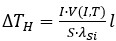 (5)
(5)
where 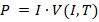 is the power dissipated as Joule heat,
is the power dissipated as Joule heat, 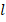 is the heat dissipation distance, and,
is the heat dissipation distance, and, 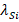 is the thermal conductivity of silicon [
is the thermal conductivity of silicon [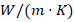 ].
].
b) Errors due to thermal and shot noise voltages
The minimum operating current of the diode is constrained by the measurement error 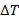 caused by the noise voltage
caused by the noise voltage 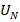 across the diode. This is calculated as:
across the diode. This is calculated as:
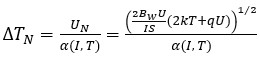 (6)
(6)
where 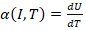 is the thermal sensitivity of the diode,
is the thermal sensitivity of the diode, 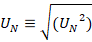 is the root mean square noise voltage determined by thermal and shot noise, and
is the root mean square noise voltage determined by thermal and shot noise, and 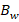 is the noise bandwidth.
is the noise bandwidth.
The error caused by noise voltage is restricted by the minimum current density such that it does not exceed the given 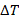 value (
value (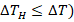 .
.
c) Total Systematic Error
The total systematic error of the diode measurement includes the self-heating error and the root mean square noise voltage error, expressed as:
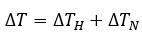 (7)
(7)
This comprehensive approach allows for a clearer understanding of the limitations and operational reliability of silicon diode temperature sensors.
Based on the criteria and equations derived, the mapping graph presented in figure 2 allows for the determination of the limiting characteristics of the sensors. The thermal sensitivity and operating temperature range of temperature sensors primarily depend on the interplay of dopant concentrations in the sensor's base region (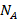 ,
,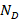 ), the operating current (
), the operating current (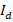 ), the temperature (
), the temperature (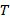 ), and several other parameters. These dependencies are typically evaluated using sensitivity curves, which consider the linear or simple nonlinear relationships among the parameters through conventional analytical methods [1,12,18-20].
), and several other parameters. These dependencies are typically evaluated using sensitivity curves, which consider the linear or simple nonlinear relationships among the parameters through conventional analytical methods [1,12,18-20].
This mapping graph visually illustrates the maximum operating temperature of the sensor using a color gradient, while contour lines indicate measurement errors. From figure 4, we can observe the following:
To increase the operating temperature of the DTS, both the dopant concentration and operating current can be maximized, enabling sensors to function at temperatures exceeding 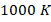 . However, doing so will result in a measurement error of
. However, doing so will result in a measurement error of 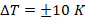 ;
;
Conversely, for a maximum operating temperature of 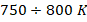 , the sensor can achieve an error of K
, the sensor can achieve an error of K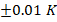 by increasing the current while using lower dopant concentrations. Alternatively, sensors can be designed for precision by further reducing the dopant concentration, allowing for operation with an accuracy of K
by increasing the current while using lower dopant concentrations. Alternatively, sensors can be designed for precision by further reducing the dopant concentration, allowing for operation with an accuracy of K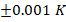 .
.
This approach, which identifies the limiting characteristics of silicon diode temperature sensors within specified measurement accuracy, is presented here for the first time. Visualizing these characteristics in a 3D format helps to clarify the intricate relationships and performance metrics involved.
This study identified the limiting characteristics that determine the maximum operating temperature and measurement accuracy of silicon diode temperature sensors. The proposed method showed that the sensors’ operating ranges could be extended by optimizing factors such as dopant concentrations and operating current. The results indicate that these diode temperature sensors can function at temperatures exceeding 1000 K with a measurement accuracy of ±10 K, or at lower temperatures with an accuracy of ±0.001 K. This significantly enhances the potential applications of these sensors in high-temperature environments, increasing their efficiency and practicality.
1 M. Mansoor, I. Haneef, S. Akhtar, A. De Luca, and F. Udrea, Sensors and Actuators A: Phys. 232 (2015) 63. https://doi:10.1016/j.sna.2015.04.022
2 S. Rao, G. Pangallo, F. Pezzimenti, and F.G.D. Corte, IEEE Electron Device Lett. 36(7) (2015) 720. https://doi:10.1109/LED.2015.2436213
3 J.Sh. Abdullayev, I.B. Sapaev, East Eur. J. Phys. 3 (2024) 344. https://doi.org/10.26565/2312-4334-2024-3-39
4 S. Santra, F. Udrea, P.K. Guha, S.Z. Ali, and I. Haneef, Microelectronics Journal 41(9) (2010) 540. https://doi:10.1016/j.mejo.2009.12.005
5 R.R. Bebitov, O.A. Abdulkhaev, D.M. Yodgorova, D.B. Istamov, G.M. Khamdamov, Sh.M. Kuliyev, A.A. Khakimov, A.Z. Rakhmatov, Low Temperature Physics 49(2) (2023) 256. https://doi:10.1063/10.0016843
6 J.Sh. Abdullayev, I.B. Sapaev, Eurasian Physical Technical Journal 21(3(49)) (2024) 21. https://doi.org/10.31489/2024No3/21-28
7 J.Sh. Abdullayev, I.B. Sapaev, Physical Sciences and Technology (Phys. sci. technol) 11(3-4) (2024) 39. https://doi.org/10.26577/phst2024v11i2b05
8 R.R. Bebitov, O.A. Abdulkhaev, D.M. Yodgorova, D.B. Istamov, Sh.M. Kuliyev, A.A. Khakimov, A.B. Bobonazarov, A.Z. Rakhmatov, Low Temperature Physics 50(5) (2024) 458. https://doi:10.1063/10.0025635
9 E.L.W. Gardner, J.W. Gardner, and F. Udrea, Sensors 23(2) (2023) 681. https://doi:10.3390/s23020681
10 M. Kimura, Lect. Notes Electr. Eng. 49 (2009) 309. http://dx.doi.org/10.1007/978-3-642-00578-7_19
11 M. Kimura and K. Toshima, Sensors and Actuators, A: Physical 108(1–3) (2003) 239. https://doi:10.1016/S0924-4247(03)00290-5
12 A. De Luca, V. Pathirana, S.Z. Ali, D. Dragomirescu, and F. Udrea. Sensors Actuators, A Phys. 222 (2015) 31. https://doi:10.1016/j.sna.2014.11.023
13 P.K. Guha, S.Z. Ali, C.C.C. Lee, F. Udrea, W.I. Milne, T. Iwaki, J.A. Covington, J.W. Gardner, Sensors Actuators, B Chem. 127(1) (2007) 260. https://doi:10.1016/j.snb.2007.07.047
14 L. Ribeiro, O. Saotome, R. d’Amore, R. de Oliveira Hansen, Sensors 22(9) (2022) 3484. https://doi.org/10.3390/s22093484
15 Y. Zhang and Y. Jiang, IEEE Sensors Journal 23(6) (2023) 5718. https://doi:10.1109/JSEN.2023.3240417
16 F. Ejeian, Sh. Azadi, A. Razmjou, Y. Orooji, A. Kottapalli, M. Ebrahimi Warkiani, M. Asadnia, Sensors and Actuators: A Phys. 295 (2019) 483. https://doi:10.1016/j.sna.2019.06.020
17 D.B. Istamov, O.A. Abdulxayev, Scientific Bulletin of NamSU 2 (2024) 39.
18 D.B. Istamov, O.A. Abdulkhaev, A.A. Khakimov, K.N. Allakulov, D.M. Yodgorova, A.Z. Rakhmatov, Uzbek Journal of Physics 26(4) (2025) 1. https://doi.org/10.52304/.v26i4.577
19 Y.M. Shwarts, V.L. Borblik, N.R. Kulish, E.F. Venger, and V.N. Sokolov, Sensors and Actuators: A Phys. 86(3) (2000) 197. https://doi:10.1016/S0924-4247(00)00445-3
20 S.S. Courts, Cryogenics 74 (2016) 172. https://doi:10.1016/j.cryogenics.2015.09.006
21 A. De Luca, V. Pathirana, S.Z. Ali, D. Dragomirescu, and F. Udrea, Sensors and Actuators: A Phys. 222 (2015) 31. https://doi:10.1016/j.sna.2014.11.023
D.B. Istamov, O.A. Abdulkhayev, Sh.M. Kuliyev, Limiting characteristics of silicon diode temperature sensors for determining the maximum temperature with specified measurement accuracy, UNEC J. Eng. Appl. Sci. 5(1) (2025) 63-69. https://doi.org/10.61640/ujeas.2025.0507
Anyone you share the following link with will be able to read this content:
M. Mansoor, I. Haneef, S. Akhtar, A. De Luca, and F. Udrea, Sensors and Actuators A: Phys. 232 (2015) 63. https://doi:10.1016/j.sna.2015.04.022
S. Rao, G. Pangallo, F. Pezzimenti, and F.G.D. Corte, IEEE Electron Device Lett. 36(7) (2015) 720. https://doi:10.1109/LED.2015.2436213
J.Sh. Abdullayev, I.B. Sapaev, East Eur. J. Phys. 3 (2024) 344. https://doi.org/10.26565/2312-4334-2024-3-39
S. Santra, F. Udrea, P.K. Guha, S.Z. Ali, and I. Haneef, Microelectronics Journal 41(9) (2010) 540. https://doi:10.1016/j.mejo.2009.12.005
R.R. Bebitov, O.A. Abdulkhaev, D.M. Yodgorova, D.B. Istamov, G.M. Khamdamov, Sh.M. Kuliyev, A.A. Khakimov, A.Z. Rakhmatov, Low Temperature Physics 49(2) (2023) 256. https://doi:10.1063/10.0016843
J.Sh. Abdullayev, I.B. Sapaev, Eurasian Physical Technical Journal 21(3(49)) (2024) 21. https://doi.org/10.31489/2024No3/21-28
J.Sh. Abdullayev, I.B. Sapaev, Physical Sciences and Technology (Phys. sci. technol) 11(3-4) (2024) 39. https://doi.org/10.26577/phst2024v11i2b05
R.R. Bebitov, O.A. Abdulkhaev, D.M. Yodgorova, D.B. Istamov, Sh.M. Kuliyev, A.A. Khakimov, A.B. Bobonazarov, A.Z. Rakhmatov, Low Temperature Physics 50(5) (2024) 458. https://doi:10.1063/10.0025635
E.L.W. Gardner, J.W. Gardner, and F. Udrea, Sensors 23(2) (2023) 681. https://doi:10.3390/s23020681
M. Kimura, Lect. Notes Electr. Eng. 49 (2009) 309. http://dx.doi.org/10.1007/978-3-642-00578-7_19
M. Kimura and K. Toshima, Sensors and Actuators, A: Physical 108(1–3) (2003) 239. https://doi:10.1016/S0924-4247(03)00290-5
A. De Luca, V. Pathirana, S.Z. Ali, D. Dragomirescu, and F. Udrea. Sensors Actuators, A Phys. 222 (2015) 31. https://doi:10.1016/j.sna.2014.11.023
P.K. Guha, S.Z. Ali, C.C.C. Lee, F. Udrea, W.I. Milne, T. Iwaki, J.A. Covington, J.W. Gardner, Sensors Actuators, B Chem. 127(1) (2007) 260. https://doi:10.1016/j.snb.2007.07.047
L. Ribeiro, O. Saotome, R. d’Amore, R. de Oliveira Hansen, Sensors 22(9) (2022) 3484. https://doi.org/10.3390/s22093484
Y. Zhang and Y. Jiang, IEEE Sensors Journal 23(6) (2023) 5718. https://doi:10.1109/JSEN.2023.3240417
F. Ejeian, Sh. Azadi, A. Razmjou, Y. Orooji, A. Kottapalli, M. Ebrahimi Warkiani, M. Asadnia, Sensors and Actuators: A Phys. 295 (2019) 483. https://doi:10.1016/j.sna.2019.06.020
D.B. Istamov, O.A. Abdulxayev, Scientific Bulletin of NamSU 2 (2024) 39.
D.B. Istamov, O.A. Abdulkhaev, A.A. Khakimov, K.N. Allakulov, D.M. Yodgorova, A.Z. Rakhmatov, Uzbek Journal of Physics 26(4) (2025) 1. https://doi.org/10.52304/.v26i4.577
Y.M. Shwarts, V.L. Borblik, N.R. Kulish, E.F. Venger, and V.N. Sokolov, Sensors and Actuators: A Phys. 86(3) (2000) 197. https://doi:10.1016/S0924-4247(00)00445-3
S.S. Courts, Cryogenics 74 (2016) 172. https://doi:10.1016/j.cryogenics.2015.09.006
A. De Luca, V. Pathirana, S.Z. Ali, D. Dragomirescu, and F. Udrea, Sensors and Actuators: A Phys. 222 (2015) 31. https://doi:10.1016/j.sna.2014.11.023