UNEC Journal of Engineering and Applied Sciences Volume 5, No 1 (2025), pages 5-15 (2025) Cite this article, 
102 https://doi.org/10.61640/ujeas.2025.0501
Composite materials have a wide range of applications and have always attracted great attention from researchers because they are lighter and stronger, resistant to corrosion and wear, and also provide design flexibility. One of the most serious disadvantages of traditional composite materials is the sharp difference between their mechanical properties at the contact surfaces, which causes them to break. Efforts to eliminate the disadvantages of traditional composite materials led to the creation of a new generation of composite materials called functionally graded materials (FGMs) as thermal shields by Japanese materials scientists in 1984 within the framework of an aerospace project. FGMs provide smooth and continuous changes in physical, chemical, and mechanical material properties such as Young's modulus, Poisson's ratio, and density from one surface to another [1-3].
Functionally graded materials have a wide range of applications. Studies on the mechanical properties and application areas of FCMs continue today [4-6]. The wide range of applications of FGMs requires the examination of the responses of structural elements made of them to various elastic environments, different loading and boundary conditions, and the revision of the resulting responses. There are many studies that examine the stability and vibration behavior of cylindrical shells made of FGMs by using their unique properties [7-14].
In most of the above studies, the stability and vibration problems of FGM cylindrical shells have been solved by using analytical or numerical methods for compressed boundary conditions, where the elastic foundation effect is not taken into account. FGM cylindrical shells are used in elastic media in industries requiring advanced technologies. The elastic medium effect can be modeled depending on several parameters, in this study, a two-parameter elastic foundation, namely the Pasternak elastic foundation model, is considered [15]. Studies on the stability of functionally graded cylindrical shells under external pressure in elastic media have attracted more attention from researchers, especially in recent years [16-21].
Literature review reveals that the studies on the analytical solution of stability problem of FGM cylindrical shells with clamped edges under external lateral compressive pressure in elastic medium are very limited. The aim of this study is to fill this gap.
The FGM cylindrical shell under lateral external pressure with thickness, radius and length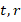 
and 
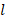, respectively, is on the Pasternak elastic foundation (figure 1). The Cartesian coordinate system is shown as 
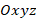and the origin is chosen at the left end of the mid-surface of the cylinder. The coordinate axes 
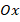and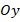 
are in the longitudinal direction and circumferential direction, respectively. The 
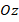axis is perpendicular to the surface where the 
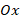and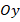 
directions are located and is directed towards the inside of the cylinder (figure 1). In the chosen coordinate system, the cylindrical shell is defined as the three-dimensional 
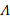region as follows:
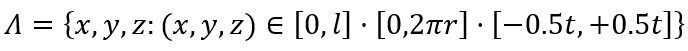(1)
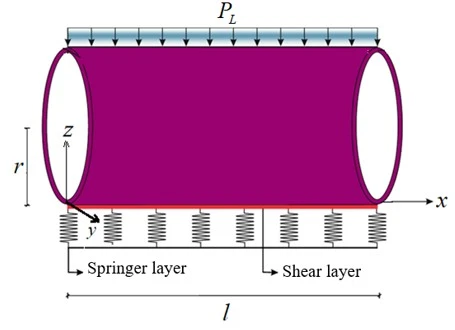
Figure 1. FGM cylindrical shell on the Pasternak elastic foundation under lateral external pressure and coordinate system
The analytical model of Pasternak elastic foundation is defined as follows [15]:
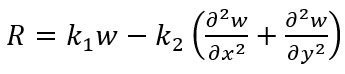(2)
where, the symbol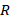 
represents the reaction force per unit area of the Pasternak elastic foundation,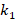 
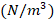is the base reaction coefficient of the elastic foundation,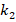 
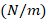is the modulus of elasticity of the shear layer whose thickness is negligible, and w represents a displacement perpendicular to the reference surface, which is very small compared to the thickness of the cylindrical shell.
The cylindrical shell on the Pasternak foundation is made of functionally graded materials. There are two basic approaches to modeling FGMs. In the first approach, the volume fraction of the ceramic or metal is assumed to be piecewise continuous and the FGM is assumed to be formed with the same volume fraction in each region, i.e., semi-homogeneous ceramic-metal layers. In the second approach, the volume fraction of the ceramic or metal is assumed to be continuous and the ceramic volume fraction can be represented as a function of the thickness coordinate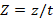 
as follows [22]:
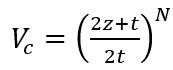(3)
where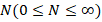 
is a volume fraction exponent that determines the material variation pattern in the direction of the FGM shell thickness and is a non-negative number. By varying the 
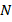exponent from this analytical expression, an infinite number of composition distributions can be generated.
In order to model the material properties of FGMs realistically, those properties need to be defined as temperature and location dependent. The Voigt model, known as a simple rule for the mixture of composite materials, can be used to obtain the mixture in question.
We can represent the effective material properties of the FGM shell as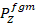 
, Young's modulus as 
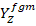and Poisson’s ratio as 
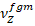and express them as the sum of the functions in the form of a power function as follows [2, 19, 22]:
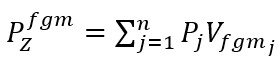(4)
where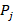 
and 
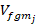are the homogeneous material properties and volume fractions of component 
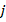, and the sum of the volume fractions of all component materials in the compositions is equal to one:
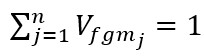(5)
The Young modulus and the Poisson's ratio of FGMs are assumed to be a nonlinear function of temperature [22]:
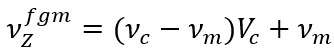(6)
where,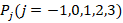 
coefficients are unique for each material and depend on the temperature T (in Kelvin (K)). Table 1 presents the mechanical properties of the components of zirconium oxide (ZrO2) and titanium aloe (Ti-6Al-4V) varieties and the mechanical properties of FGMs formed from their mixtures using the expression (6).
For the FGM consisting of a mixture of two materials such as metal and ceramic, the expressions in the form of force functions for the effective Young modulus and the effective Poisson's ratio are easily obtained from equations (4) and (5) as a special case as follows:
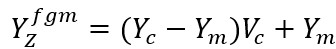(7)
and
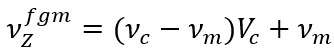(8)
The ratio of the effective Young modulus of FGM to the Young modulus of the metal (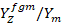
) for the volume fraction index 
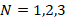, as the dimensionless 
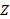and 
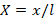coordinates change in the intervals 
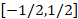and 
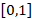, respectively, are drawn with the MAPLE 14 program and are presented in figure 2 using analytical expression (7). In all figures, the vertical axis (
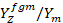) represents the ratio, and the horizontal axes 
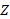and 
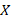represent the dimensionless thickness and length coordinates, respectively.
The basic relations of cylindrical shells made of FGMs within the framework of Kirchhoff-Love theory can be expressed as follows [8, 22]:
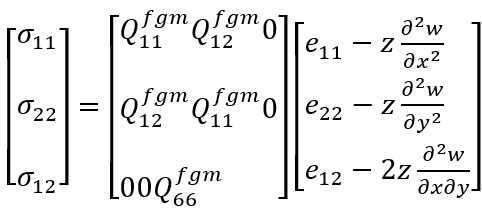(9)
where,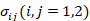 
are the stress components, 
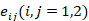are the strain components at the mid-surface of the FGM cylindrical shell, and 
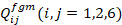are the coefficients depending on the properties of the FGM cylindrical shells and are found from the following expressions:
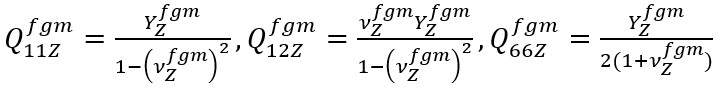(10)
The expression of force and moment components are carried out with the following integrals [23]:
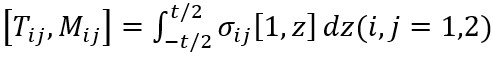(11)
The representation of force components and Airy stress function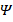 
is carried out as follows [8, 22]:
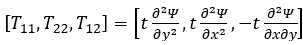(12)
If we assume that the FGM cylindrical shell is subjected to the uniform lateral external pressure, the mathematical model of the expressions for the initial moment-free membrane force components on the reference surface are as follows (figure 1):
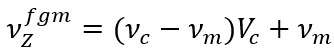(13)
As the expressions (2), (7)-(9) and (11) are used, the final form of the basic equations of the FGM cylindrical shells under uniform lateral pressure on the Pasternak elastic foundation are obtained as follows:
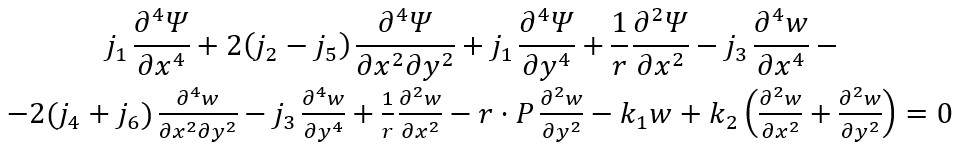(14)
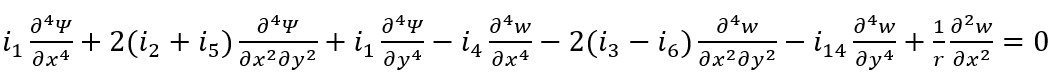(15)
where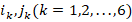 
are coefficients depending on the FGM properties and cylindrical shell characteristics.
Assume that the FGM cylindrical shell is subject to clamped boundary conditions at its edge ends. The analytical expression for the clamped boundary conditions is defined as:
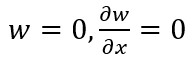(16)
The clamped boundary conditions are provided by the following approximation functions corresponding to the deflection and Airy stress functions [9]:
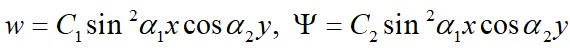(17)
where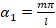 
and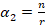 
are parameters which 
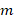and 
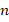represent wave numbers in the longitudinal and circumferential directions and 
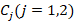represents the unknown amplitudes of the deflection and Airy stress functions, respectively.
After multiplying the strain compatibility and stability equations defined by (14) and (15) by the weight function and applying the Galerkin procedure in the Λ=(x,y):-0.5l≤x≤0.5l,0≤y≤2πr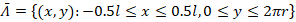
region and after some mathematical operations, the following analytical formula is obtained for the critical external lateral pressure of the FG cylindrical shells clamped at both ends on the Pasternak elastic foundation:
In numerical analysis, functionally graded materials are mixtures of metal and ceramic, consisting of Ti-6Al4V and ZrO2 and are called Ti-6Al4V/ZrO2. Table 1 presents the mechanical properties of those materials and their components.
Table 2 presents the distributions of the DCELP for ZrO2, FGM-quadratic profile (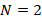
) and Ti-6Al-4V cylindrical shells with and without elastic foundations, depending on the increase of the 
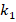and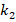 
. The geometric parameters of the cylindrical shell are considered as 
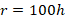and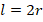 
.
As the critical lateral pressure of the FGM-quadratic profiled cylindrical shell are compared with the critical lateral load values of the ZrO2 profiled cylindrical shell, the influence of FGM-quadratic schema on the DCELP is (+24.1%) in the soilless case. That influence weakens depending on the increase of the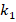 
and 
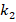. For example, at 
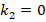and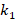 
increases from 
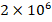to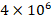 
, the influence of the FGM-quadratic profile on the DCELP decreases from 22.9% to 22.1%, while at 
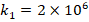and 
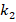increases from 
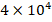to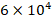 
, that influence decreases from 22.1% to 21.6%. Similarly, at 
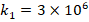and as the 
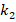increases from 
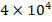to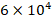 
, the effect of the FGM-quadratic model on the DCELP reduces from 21.6% to 21.2%, while at 
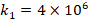and 
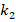increases from 
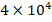to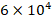 
, that effect on the DCELP reduces from 21.3% to 20.9%.
When the DCELP values of the FGM-quadratic profiled cylindrical shell are compared with DCELP values of the Ti-6Al4V profiled cylindrical shell, the influence of FGM schema on the DCELP is (-20.8%) in the soilless case. That effect generally weakens depending on the increase of the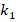 
and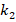 
. For example, when 
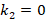and 
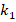increases from 
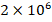to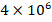 
, the effect of the FGM-quadratic profile on the DCELP decreases from (-19.8%) to (-18.7%), while as 
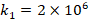and 
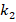increases from 
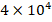to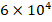 
, that influence decreases from (-18.4%) to (-18.1%). Similarly, at 
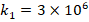and
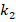increases from 
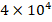to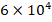 
, the influence of the FGM-quadratic schema on the DCELP decreases from (-17.9%) to (-17.6%), k1=4×106
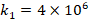and 
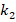increases from 
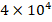to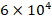 
, the influence of the FGM schema decreases from (-17.4%) to (-16.9%).
It is seen that the ground effect on the values of DCELP of the Ti-6Al4V/ZrO2 profiled cylindrical shells increases versus the increase of the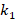 
and 
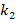. For example, at 
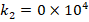and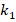 
increases from 
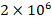to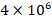 
, the ground effect on the values of DCELP increases from 4.9% to 9.0%, from 6.5% to 11.8% and from 7.3% to 13.7% for the cylindrical shells with ZrO2, FGM-quadratic and Ti-6Al4V schemes, respectively. Similarly, at 
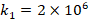and k2
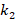increases from 
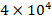to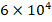 
, the ground effect on the values of the DCELP increases from 9.2% to 11.4%, from 12.1% to 15.0% and from 14.3% to 17.5% for the for the cylindrical shells with ZrO2, FGM-quadratic and Ti-6Al4V schemes, respectively. In addition, at 
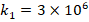and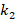 
rises from 
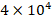to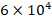 
, it is seen that the ground effect on the DCELP values increases from 11.2% to 13.4%, from 14.7% to 17.6% and from 17.5% to 20.8% in ZrO2, FGM and Ti-6Al4V cylindrical shells, respectively. Finally, at 
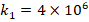and 
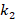increases from 
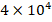to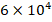 
increases from to, it is seen that the ground effect on the DCELP increases from 13.2% to 15.4%, from 17.4% to 20.3% and from 20.8% to 24.3% in ZrO2, FGM and Ti-6Al4V profiled cylindrical shells, respectively. It is also seen that the percentage values of the ground effect on the DCELP values generally decrease depending on the increase of the 
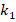and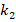 
.
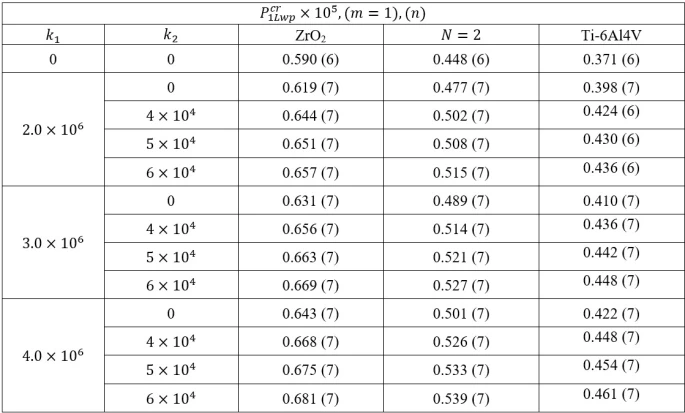
Table 2. Variations of the values of DCELP for ZrO2, FGM-quadratic, Ti-6Al-4V cylindrical shells versus the elastic foundation coefficients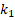 
and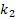 
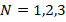) and Ti-6Al-4V cylindrical shells with and without elastic foundation versus the 
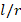with the 
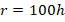, and for the 
, 
, 
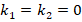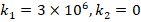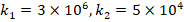. When we examine the changes of DCELP values of FGM cylindrical shells with and without ground with respect to 
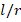, as can be seen from table 3 and figures 3-7, a decreasing trend is observed in DCELP values of Ti-6Al-4V, ZrO2 and three types (
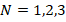) of FGM cylindrical shells as the 
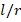increment. In addition, in grounded and ungrounded cases, the (n) wave number corresponding to the DCELP values of cylindrical shells with the Ti-6Al-4V, ZrO2 and different FGM schemes generally decreases as the 
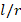increases. In all 
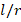ratio, the largest DCELP values are obtained in the ZrO2 cylindrical shell, while the smallest in the Ti-6Al-4V cylindrical shell. When we examine the varying FGM cylindrical shells among themselves, the smallest DCELP values are obtained at 
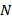=3 and the largest values are obtained at 
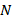=1.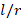
ratio from 1 to 3. For example, in the cases of 
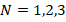, the effects of FGM schemes on DCELP values vary between 19.5% and 19.7%, 24% and 24.01%, and 25.9% and26.1%, respectively. In the grounded case, the effects of the profiles on DCELP in all of the FGM model cylindrical shells defined as 
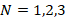are weakened as the 
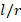ratio increases. For example, the effects of FGM profiles on DCELP decrease from 19.3% to 17.6%, from 23.6% to 21.2% and from 25.4% to 22.7%, respectively for 
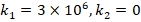, while that effect decreases from 18.9% to 16.5%, from 23% to 19.8% and from 24.8% to 21.3%, respectively for
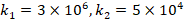as 
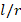increases from 1 to 3.
In the groundless case, when the DCELP values of the FGM cylindrical shell are compared with the DCELP values of the Ti-6Al-4V model cylindrical shell, it is seen that the FGM-profiles effects change weakly depending on the increase of the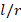 
ratio from 1 to 3. For example, in the cases of 
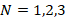, the effects of FGM schemes on DCELP values vary between (-27.8%) and (-28.2%), (-20.9%) and (-21.0%) and (-17.9% - (-18.2%), respectively, as 
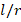increases from 0.5 to 3. In the grounded case, the effects of the profiles on DCELP in all of the FGM cylindrical shells defined as N=1, 2 and 3 decrease as the 
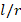increases. For example, at as 
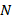=1, 2 and 3, the effects of FGM profiles on DCELP increase from (-27%) to (-22.9%), from (-20.3%) to (-17.6%) and from (-17.4%) to (-15.3%), respectively for the 
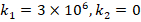, while those effects decrease from (-25.8%) to (-20.8%), from (-19.5%) to (-16.0%) and from (-16.77%) to (-13.9%), respectively, for the 
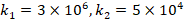, as 
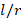increases from 1 to 3.
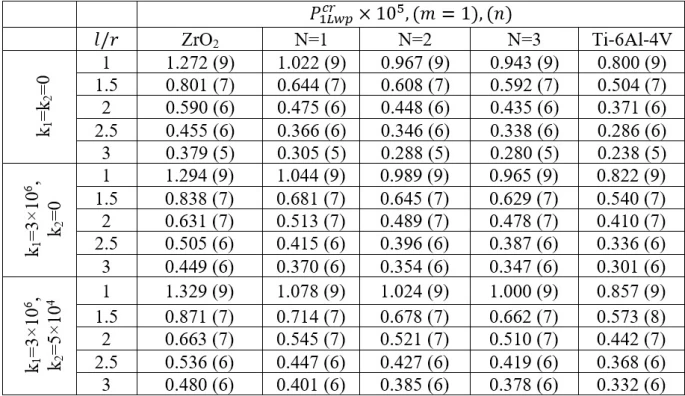
Table 3. Variations of the values of DCELP for ZrO2, FGM-quadratic, Ti-6Al-4V cylindrical shells on the elastic foundations versus the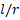 
It is observed that the Pasternak and Winkler foundation effects on DCELP values of metal, ceramic and FGM profiled cylindrical shells increase with the increase of l/r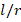
. For example, while the ground effect on DCELP values increases from 1.73% to 18.5% at k1=3×106,k2=0
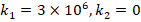in ZrO2 cylindrical shell, that effect increases from 4.5% to 26.7% when k1=3×106,k2=5×104
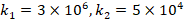, as l/r
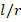increases from 1 to 3. If we examine the Ti-6Al4V cylindrical shell, while the ground effect on DCELP values increases from 2.8% to 26.5% at k1=3×106,k2=0
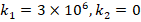, that effect increases from 7.2% to 39.5% at k1=3×106,k2=5×104
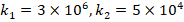, as l/r
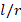increases from 1 to 3. If we look at the cases of FGM modeled cylindrical shells, at N
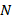=1, 2 and 3, the ground effects on DCELP values increase from 2.2% to 21.3%, from 2.3% to 22.9% and from 2.3% to 23.9%, respectively for k1=3×106,k2=0
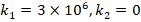, while those effects increase from 5.5% to 31.5%, from 5.9% to 33.7% and from 6.1% to 35%, respectively for k1=3×106,k2=5×104
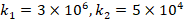, as l/r
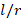increases from 1 to 3. It is also seen that as the L/R ratio increases, the percentage values of the ground effects on DCELP values for the Pasternak elastic foundation are higher than the percentage values in the Winkler elastic foundation.
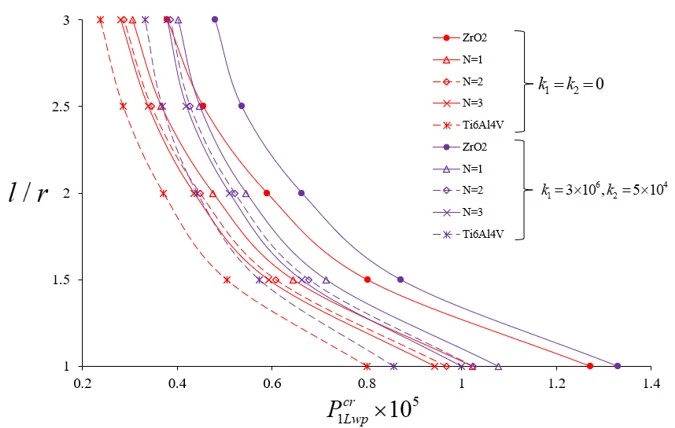
Figure 3. Distributions of the DCELP for cylindrical shells consisting of ZrO2, FGM- profiles (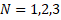
) and Ti-6Al-4V with and without Pasternak elastic foundation versus the 
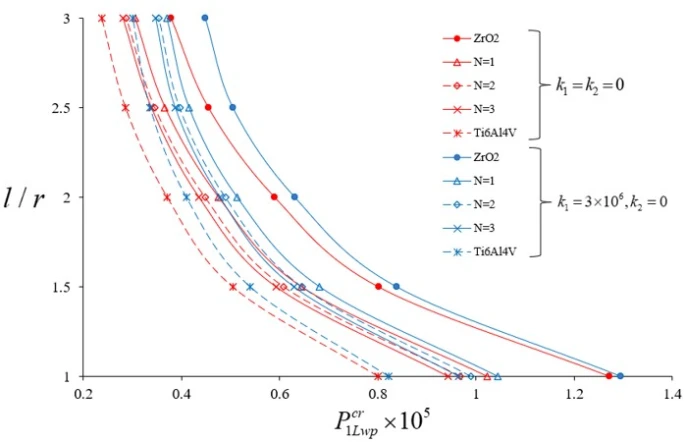
Figure 4. Distributions of the DCELP for cylindrical shells consisting of ZrO2, FGM- profiles (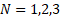
) and Ti-6Al-4V with and without Winkler elastic foundation versus the 
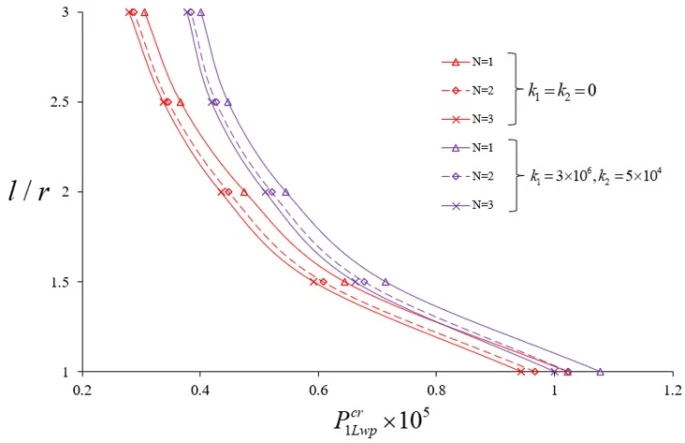
Figure 5. Distributions of the DCELP for cylindrical shells consisting of FGM- linear, quadratic and cubic profiles with and without elastic foundation versus the 
In the study, stability problem of cylindrical shells consisting of FGMs in an elastic medium under external lateral pressure within the framework of Donnell type shell theory is solved. First, general and basic information about the properties, advantages and application areas of functionally graded materials are determined. After the functionally graded materials, elastic foundation and external pressure are mathematically modeled, the basic relations of FGM cylindrical shells are established. Then, the stability and deformation compatibility equations of FGM cylindrical shells on Pasternak-Winkler elastic foundation are derived based on Kirchhoff-Love shell theory. After the approximation functions for the clamped boundary conditions are determined, Galerkin procedure is applied for the solution of the basic partial differential equations. From the algebraic equations obtained after integration, the analytical expression for the critical external lateral pressure of functionally graded cylindrical shells under clamped boundary conditions on the Pasternak elastic foundation is obtained. When the elastic medium effect is not taken into account, the analytical expression for the critical lateral external pressure of FGM cylindrical shells is obtained as a special case. The expressions in question will be minimized according to the buckling mode and the minimum values of DCELP with and without elastic media are obtained numerically. Finaly, numerical analyses, interpretations and generalizations are carried out for the minimum values of DCELP by considering different volume fractions, elastic foundation coefficients and geometric characteristics of cylindrical shells.
1 M. Koizumi, The concept of FGM ceramic transactions. ceramic transactions: functionally gradient materials 34 (1993) 3
2 Y. Miyamoto, W.A. Kaysser, B.H. Rabin, A. Kawasaki, R.G. Ford, Functionally Graded Materials: Design, Processing and Applications, Springer, New-York (1999) 330p. https://doi.org/10.1007/978-1-4615-5301-4
3 K. Ichikawa, T.S. Hirano, Functionally Graded Materials In the 21st Century: A Workshop on Trends and Forecasts. Springer, New-York (2001) 242p. https://doi.org/10.1007/978-1-4615-4373-2
4 A.H. Sofiyev, Composite Structures 211 (2019) 301. https://doi.org/10.1016/j.compstruct.2018.12.047
5 A. Garg, M.O. Belarbi, H.D. Chalak, A. Chakrabarti, Composite Structures 258 (2021) 113427. https://doi.org/10.1016/j.compstruct.2020.113427
6 D.V. Doan, P.V. Van Minh, T.V. Ke, N.T.C. Nhung, D.V. Thom, Journal of Vibration Engineering & Technologies 13 (2025) 68. https://doi.org/10.1007/s42417-024-01691-8
7 H.S. Shen, Composites Science and Technology 62 (7–8) (2002) 977. https://doi.org/10.1016/S0266-3538(02)00029-5
8 A.H. Sofiyev, Composite Structures 89(3) (2009) 356. https://doi.org/10.1016/j.compstruct.2008.08.010
9 A.H. Sofiyev, Journal of Composite Materials 45(7) (2011) 771. https://doi.org/10.1177/0021998310373515
10 A.H. Sofiyev, N. Fantuzzi, Alexandria Engineering Journal 64 (2023) 141. https://doi.org/10.1016/j.aej.2022.08.024
11 P.M. Vuong, N.D. Duc, Archives of Civil and Mechanical Engineering 23 (2023) 207. https://ui.adsabs.harvard.edu/link_gateway/2023ACME...23..207V/doi:10.1007/s43452-023-00743-2
12 L.X. Peng, S.Y. Chen, D.Y. Wei, W. Chen, Y.S. Zhang, Composite Structures 290 (2022) 115482. https://doi.org/10.1016/j.compstruct.2022.115482
13 H.V. Tung, N.V. Thinh, AIAA Journal 63 (5) (2024) 1. https://doi.org/10.2514/1.J064613
14 B. Tomczyk, M. Gołąbczak, V. Bagdasaryan, Composite Structures 356 (2025) 118890. https://doi.org/10.1016/j.compstruct.2025.118890
15 P.L. Pasternak, On a New Method of Analysis of an Elastic Foundation by Means of Two Foundation Constants, Gosudarstvennoe Izdatelstvo Literaturi po Stroitelstvu I Arkhitekture, Moscow (1954). https://doi.org/10.4236/ojce.2019.92009
16 E. Bagherizadeh, Y. Kiani, M.R. Eslami, Composite Structures 93(11) (2011) 3063. https://doi.org/10.1016/j.compstruct.2011.04.022
17 A.H. Sofiyev, F. Kadioglu, I.A. Khalilov, H.M. Sedighi, T. Vergul, R. Yenialp, On the torsional buckling moment of cylindrical shells consisting of functionally graded materials resting on the pasternak-type soil. SOCAR Proceedings 1 (2022) 16. http://dx.doi.org/10.5510/OGP2022SI100695
18 J.R. Cho, Structural Engineering and Mechanics 88(5) (2023) 439. https://doi.org/10.5510/OGP2022SI100695
19 L. Kurpa, F. Pellicano, T. Shmatko, A. Zippo, Mathematical and Computational Applications 29(1) (2024) 1. http://dx.doi.org/10.3390/mca29010010
20 H.V. Tung, N.V. Thinh, Acta Mechanica 236(2) (2025) 1091. http://dx.doi.org/10.1007/s00707-024-04207-3
21 H.S. Shen, Functionally Graded Materials: Nonlinear Analysis of Plates and Shells. 1st ed. CRC Press, Florida, (2011) 280p. https://doi.org/10.1201/9781420092578
22 M.R. Eslami, Buckling and Postbuckling of Beams, Plates and Shells, Springer, Switzerland, (2018) 588p. http://dx.doi.org/10.1007/978-3-319-62368-9
K. Ertunç, H. Dilmac, A.H. Sofiyev, Investigation of stability behavior of clamped functionally graded cylindrical shells in elastic medium under lateral pressure, UNEC J. Eng. Appl. Sci. 5(1) (2025) 5-15. https://doi.org/10.61640/ujeas.2025.0501
Anyone you share the following link with will be able to read this content:
M. Koizumi, The concept of FGM ceramic transactions. ceramic transactions: functionally gradient materials 34 (1993) 3
Y. Miyamoto, W.A. Kaysser, B.H. Rabin, A. Kawasaki, R.G. Ford, Functionally Graded Materials: Design, Processing and Applications, Springer, New-York (1999) 330p. https://doi.org/10.1007/978-1-4615-5301-4
K. Ichikawa, T.S. Hirano, Functionally Graded Materials In the 21st Century: A Workshop on Trends and Forecasts. Springer, New-York (2001) 242p. https://doi.org/10.1007/978-1-4615-4373-2
A.H. Sofiyev, Composite Structures 211 (2019) 301. https://doi.org/10.1016/j.compstruct.2018.12.047
A. Garg, M.O. Belarbi, H.D. Chalak, A. Chakrabarti, Composite Structures 258 (2021) 113427. https://doi.org/10.1016/j.compstruct.2020.113427
D.V. Doan, P.V. Van Minh, T.V. Ke, N.T.C. Nhung, D.V. Thom, Journal of Vibration Engineering & Technologies 13 (2025) 68. https://doi.org/10.1007/s42417-024-01691-8
H.S. Shen, Composites Science and Technology 62 (7–8) (2002) 977. https://doi.org/10.1016/S0266-3538(02)00029-5
A.H. Sofiyev, Composite Structures 89(3) (2009) 356. https://doi.org/10.1016/j.compstruct.2008.08.010
A.H. Sofiyev, Journal of Composite Materials 45(7) (2011) 771. https://doi.org/10.1177/0021998310373515
A.H. Sofiyev, N. Fantuzzi, Alexandria Engineering Journal 64 (2023) 141. https://doi.org/10.1016/j.aej.2022.08.024
P.M. Vuong, N.D. Duc, Archives of Civil and Mechanical Engineering 23 (2023) 207. https://ui.adsabs.harvard.edu/link_gateway/2023ACME...23..207V/doi:10.1007/s43452-023-00743-2
L.X. Peng, S.Y. Chen, D.Y. Wei, W. Chen, Y.S. Zhang, Composite Structures 290 (2022) 115482. https://doi.org/10.1016/j.compstruct.2022.115482
H.V. Tung, N.V. Thinh, AIAA Journal 63 (5) (2024) 1. https://doi.org/10.2514/1.J064613
B. Tomczyk, M. Gołąbczak, V. Bagdasaryan, Composite Structures 356 (2025) 118890. https://doi.org/10.1016/j.compstruct.2025.118890
P.L. Pasternak, On a New Method of Analysis of an Elastic Foundation by Means of Two Foundation Constants, Gosudarstvennoe Izdatelstvo Literaturi po Stroitelstvu I Arkhitekture, Moscow (1954). https://doi.org/10.4236/ojce.2019.92009
E. Bagherizadeh, Y. Kiani, M.R. Eslami, Composite Structures 93(11) (2011) 3063. https://doi.org/10.1016/j.compstruct.2011.04.022
A.H. Sofiyev, F. Kadioglu, I.A. Khalilov, H.M. Sedighi, T. Vergul, R. Yenialp, On the torsional buckling moment of cylindrical shells consisting of functionally graded materials resting on the pasternak-type soil. SOCAR Proceedings 1 (2022) 16. http://dx.doi.org/10.5510/OGP2022SI100695
J.R. Cho, Structural Engineering and Mechanics 88(5) (2023) 439. https://doi.org/10.5510/OGP2022SI100695
L. Kurpa, F. Pellicano, T. Shmatko, A. Zippo, Mathematical and Computational Applications 29(1) (2024) 1. http://dx.doi.org/10.3390/mca29010010
H.V. Tung, N.V. Thinh, Acta Mechanica 236(2) (2025) 1091. http://dx.doi.org/10.1007/s00707-024-04207-3
H.S. Shen, Functionally Graded Materials: Nonlinear Analysis of Plates and Shells. 1st ed. CRC Press, Florida, (2011) 280p. https://doi.org/10.1201/9781420092578
M.R. Eslami, Buckling and Postbuckling of Beams, Plates and Shells, Springer, Switzerland, (2018) 588p. http://dx.doi.org/10.1007/978-3-319-62368-9
UNEC Journal of Engineering and Applied Sciences 
ratio for (a) 
, (b) 
and (c) 