Anisotropic thermoelectrics based on an extruded sample of Bi0.85Sb0.15 solid solution doped with tellurium

Abstract

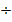The effects of tellurium impurities and heat treatment on the anisotropy of the electrical and thermal properties of extruded samples of the Bi0.85Sb0.15 solid solution in the range of ~77 300K and magnetic field strengths H up to ~74x104 A/m are studied. It was found that in extruded samples doped with tellurium and subjected to heat treatment, electrons scatter more strongly in the perpendicular direction of extrusion than in the direction of the extrusion axis, and during annealing, the increase in mobility, electrical conductivity and thermal conductivity in the direction parallel to the extrusion axis is greater than in the perpendicular direction. Therefore, in samples that have undergone annealing, the anisotropy s at ~77 K is opposite to that of samples that have not undergone annealing. In annealed samples of Bi0.85Sb0.15 with 0.001 at.% tellurium, the absolute values ​​of α in the perpendicular direction of the extrusion axis are more sensitive to the magnetic field than in the parallel direction, and the anisotropy of the thermoelectric power (Dα) at ​​a magnetic field strength of H=42x104A/m reaches the value Dα=80 kV/K at ~77K.

Introduction

One of the important issues in materials science for alternative energy converters is to improve the relevant parameters of the materials used in the manufacture of these energy converters [1-4]. Single crystals of solid solutions of Bi-Sb systems, especially high strength extruded samples of these systems, are the most effective material for creating various thermo- and magneto-thermoelectric energy converters [5-13]. In industrial applications of thermoelectric power converters, a significant increase in their efficiency and suitability is necessary, which is associated with the efficiency and mechanical strength of the thermoelectric material used. The quality factor (efficiency) of thermoelectric converters directly depends on the quality factor (Z) of the thermoelectric material used in them [14-25]. Anisotropic thermoelectric converters, in contrast to conventional converters, have lower efficiency, but allow obtaining significant electromotive forces (e.m.f.) at small temperature differences. Therefore, anisotropic thermoelements (ATE) are used in calorimetric devices and heat meters, being characterized by exceptionally high speed [26-28].
Bismuth monocrystals are the classical material for ATE in terms of the thermoelectric power Dα, which is due to the strongly anisotropic contribution of T holes to the electrical conductivity. Differential thermopower in bismuth single crystals Dα= 40¸ 50 μV/K in the temperature range from ~80K to the melting point. The constancy of Dα in a wide temperature range is a great advantage for the use of such ATEs for metrological purposes, but the small value of Dα does not allow obtaining a high volt-watt sensitivity, and at best, when used on calorimetric cells, it gives a value of 10 ¸25 μV/K [29]. Bi-Sb alloys are a thermoelectric material with a highly anisotropic electric spectrum of electrons in the L zone [30]. Therefore, mechanically strong extruded samples of Bi-Sb solid solutions are a promising material for the creation of ATE as part of various electronic devices [31].
In it was experimentally established that it is possible to increase Da in solid solutions of Bi-Sb systems in a transverse magnetic field [32]. The use of a transverse magnetic field makes it possible to significantly increase the value of Da both in pure bismuth and in Bi-Sb alloys.
By doping the Bi0.85Sb0.15 solid solution, one can achieve an increase in the concentration of electrons, which are the main charge carriers in this material. Bismuth and bismuth-antimony alloys have a layered structure; therefore, charge carriers scatter differently in different a direction, which leads to anisotropy of electrical and thermal parameters. The study of the influence of various impurities on the anisotropy of the electrical properties of solid solutions of Bi-Sb systems in a wide range of temperatures and magnetic fields for the creation of more efficient ATEs is topical.
Bismuth, antimony and their solid solutions have a very peculiar energy spectrum, the structure of which is easily changed under the influence of various factors. In this sense, and also taking into account the high mobility of carriers and the anisotropy of physical properties, bismuth and alloys based on it are unique objects of research, which lead to wide practical applications of these materials and devices based on them.
Considering the above, in this work, in order to clarify the effect of tellurium impurities and heat treatment on the anisotropy of the electrical and thermal properties of extruded samples of the Bi0.85Sb0.15 solid solution, its extruded samples with different concentrations of tellurium impurities were obtained and their electrical conductivity (s), thermopower coefficients ( α), Hall (RH) and thermal conductivity (χ) in the range of ~77 300K and magnetic field strength up to ~74x104 A/m in the parallel and perpendicular direction of the extrusion axis.

Experimental part

Extruded samples of Bi0.85Sb0.15 ˂Te˃ solid solutions were obtained in the following technological sequence: composition synthesis from initial components; mechanical grinding of the alloy in a porcelain mortar and selection of a fraction with a particle size of £ 0.63 mm using a sieve; production of briquettes with a diameter of ~30 mm from it by cold pressing at ~300K and a pressure of ~3.5 T/cm2 for the next stage; extrusion of fine billets (briquettes). The synthesis was carried out by direct co-fusion of the components. The starting materials were placed in a stoichiometric ratio into a quartz ampoule, which had been preliminarily etched in a chromic acid solution (K2Cr2O7 + H2SO4) and washed with distilled water. Due to the fact that the thermoelectric properties of low-temperature materials significantly depend on the degree of purity of the components, the initial components of bismuth grade "Vi-0000" and antimony grade "Su-0000" were subjected to preliminary purification. Distilled (or doubly sublimated) tellurium T-sCh was used as dopants. Impurities and starting components were weighed with an accuracy of ±0.0001 g. The dopant Te was introduced during synthesis. Samples with a low tellurium concentration were obtained by fusing an appropriate amount of a Bi0.85Sb0.15 sample with a concentration of 0.1 at. % Te with a Bi0.85Sb0.15 sample. The synthesis was carried out in quartz ampoules evacuated to  ~10-3Pa at ~ 673K ​​for 2 hours. During the synthesis, the ampoule with the substance was constantly subjected to rocking. The ampoule with the synthesized substance was abruptly cooled to room temperature by dipping into water. In the process of extrusion, the technological parameters of extrusion (temperature, drawing speed, etc.) were chosen such that the formation of extruded bars took place under superplasticity conditions without macro- and micro-disturbances. The bending strength of the obtained extruded samples is ~3 times higher than the strength of single-crystal samples of this composition.
Extrusion was carried out on an MS-1000 hydraulic press from a diameter of ~30 mm to a diameter of ~6 mm using special equipment. Technological parameters of extrusion were: Tex.=475 ±3K; Pex= 480MPa, press travel speed vpr= 0.02 cm/min, drawing ratio -25.
The texture of Bi0.85Sb0.15˂Te˃ samples was studied using the XR D8 ADVANCE X-ray facility, Bruker, Germany, by the method described in [33]. X-ray diffraction patterns were recorded at room temperature using a D2 Phaser diffractometer, Bruker. Using the TOPAS-4.2 program, it was confirmed from the obtained diffraction patterns that the samples are powders of the Bi0.85Sb0.15 solid solution, which crystallizes in the hexagonal syngony.
The interplanar distances of bismuth, antimony and their solid solutions along the main lines are close to each other, so the determination of the phase composition was carried out using bismuth grade "Vi-0000".
From the obtained bars on the A207.40M installation, samples were cut out for research in the form of a parallelepiped with dimensions of 3×5×12 mm by the method of electric spark cutting. The damaged layer formed on the sample surface during cutting was removed by electrochemical etching in a KOH+C4H4O6+H2O solution described in [{ref:34}]. Samples were annealed in quartz ampoules evacuated to a pressure of ~10-3Pa at a temperature of ~503K for 5 hours.
Electrical and thermal parameters were measured by the method described in along and perpendicular to the direction of the extrusion axis [35]. The error in measuring electrical parameters and thermal conductivity does not exceed ~3% and ~5%, respectively.

Results and discussion

Samples that did not undergo heat treatment after extrusion and the same samples that underwent annealing were studied. The results obtained are presented in figures 1-5 and in tables 1-3. The figures and tables show the absolute values ​​of the thermopower (α) and Hall (RH) coefficients.
It can be seen from the figures that adding tellurium in an amount of 10-4¸10-1 at.% to the investigated solid solution significantly reduces the resistivity (ρ) in the parallel and perpendicular direction of extrusion relative to the undoped Bi0.85Sb0.15 sample. A particularly strong change occurs at low temperatures, where the impurity conductivity prevails. As the temperature increases, the influence of tellurium atoms on ρ weakens. A similar effect of tellurium is also observed on the thermopower α and Hall RH coefficients.
The change in ρ of samples of the Bi0.85Sb0.15 solid solution with low tellurium concentrations that have undergone heat treatment is more sensitive to the magnetic field than samples that have not undergone heat treatment. At high tellurium concentrations, the effect of tellurium impurities and magnetic field (magnetoresistance) on the resistivity of samples that have undergone and have not undergone heat treatment are almost the same. In samples with concentrations of 0.05 and 0.1 at. % Te in annealed and unannealed samples, there are almost no magnetic resistances.
In all cases, at ~77 K, heat treatment leads to a decrease in electrical resistance and an increase in the Hall coefficient in the absence of a magnetic field in parallel and perpendicular directions of the extrusion axis, except for the sample with 0.001 at% tellurium. In samples with 0.1 at.% tellurium, the effect of heat treatment on ( ), (α) and (RH)is strongly weakened (figure 1).
Heat treatment leads to a decrease in the concentration of structural defects in Bi0.85Sb0.15 samples that occur during plastic deformation of the crystal lattice in individual grains, an increase in μ and an increase in the prevalence of current carrier scattering on lattice vibrations (figure 2).
In extruded samples, there are difficult-to-anneal defects that cause changes in the concentration of current carriers and their mobility. Such defects can be twin boundaries, stacking faults that occur during plastic deformation.

Figure 1. Dependences of electrical conductivity s (a, b), thermopower α (c, d) and Hall RH (e, f) coefficients of extruded samples of the Bi0.85Sb0.15 solid solution on temperature: a, c, e - not passed, b, d, f - heat treated; 1 and 2 unalloyed samples, 3-12 samples doped 0.0001; 0.0005; 0.001; 0.005; 0.1 at.% Te, respectively; 1,3,5,7,9,11 - measurements along the axis, 2,4,6,8,10,12 - perpendicular to the extrusion axis

a                                                                                                   b

Full size image

c                                                                             d

Full size image

e                                                                              f

Full size image

During heat treatment of textured Bi0.85Sb0.15 samples, recrystallization occurs in them, i.e., a change in the nature of the texture. To obtain a given texture, and hence a given level of anisotropy of properties, it is necessary to know the regularities of texture formation under various influences [11,27].

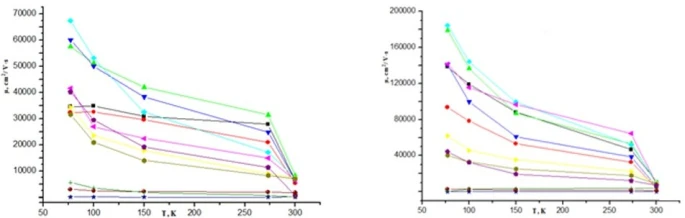
Figure 2. Dependence of the Hall mobility μ. extruded samples of the Bi0.85Sb0.15 solid solution on temperature Designations are the same as in figure 1

a                                                                               b

Full size image

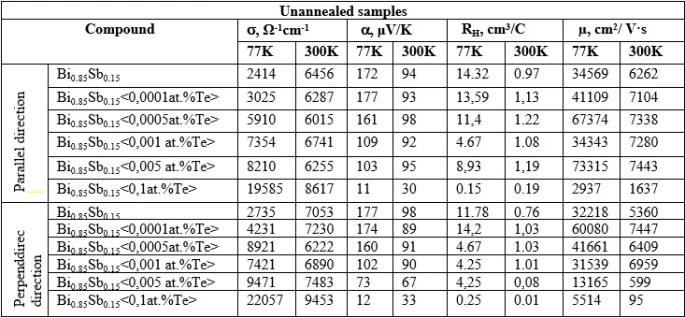
Table 1. Electrical parameters of extruded samples of the Bi0.85Sb0.15˂Te˃ solid solution in the parallel and perpendicular directions

Full size image

Full size image

Heat treatment at ~503K leads to an increase in electrical conductivity and the Hall coefficient. A slight change in α during heat treatment apparently indicates that the change in RH during heat treatment is mainly due to a change in the parameter characterizing the mechanism of electron scattering in the material. It also follows from this that the defects that appear in Bi0.85Sb0.15 during extrusion are mainly non-electroactive.
The electrical parameters of the extruded samples of the Bi0.85Sb0.15 solid solution have a noticeable anisotropy with respect to the extrusion axis. In unalloyed and unannealed samples, s in the absence of a magnetic field in the entire temperature range in the direction perpendicular to the extrusion axis s^ is higher than in the direction of the extrusion axis sêê. After annealing, this ratio is reversed; anisotropy s changes its sign. At low concentrations of tellurium atoms, the anisotropy s at ~77K and in the absence of a magnetic field in samples without heat treatment is greatly weakened.
Moreover, in all cases in a magnetic field sêê˃s^. At high tellurium concentrations, the anisotropy s and its dependence on the magnetic field weaken even more. In alloys with an antimony content of less than 8.5 at.%, the contribution to the electrical conductivity is mainly made by holes Т4̅5 for alloys with 8.5 ˂х ˂ 15 Ls holes [36,37].
For alloys with an antimony concentration of more than 11 at%, the contribution of T4̅5 holes to s drops sharply, and s is practically carried out due to transitions between the Ls and La extrema, which has a low density of states. This leads to a sharp increase in ρ. With a further increase in the concentration of antimony in the solid solution near nitrogen temperatures, a decrease in the value of ρ is observed, although the width of the forbidden gap still continues to increase. This is due to the fact that ∑-holes rise in the valence band and their contribution reduces the value of ρ [38].
It follows from tables 1- 3 that the electrical and thermal parameters of the extruded samples of the Bi0.85Sb0.15 solid solution, undoped and doped with different tellurium concentrations, have a noticeable anisotropy relative to the extrusion axis.
When alloying extruded Bi0.85Sb0.15 samples up to 0.1 at.% with tellurium, which have not undergone heat treatment, in the samples in the absence of a magnetic field in the entire temperature range, the conductivity in the perpendicular direction of extrusion s^ is higher than in the direction parallel to the extrusion axis sê. After annealing, this ratio is reversed; the anisotropy of electrical conductivity in undoped samples and samples with different concentrations of tellurium changes its sign. When alloying extruded Bi0.85Sb0.15 samples up to 0.1 at.% with tellurium, which have not undergone heat treatment, in the samples in the absence of a magnetic field in the entire temperature range, the conductivity in the perpendicular direction of extrusion s^ is higher than in the direction parallel to the extrusion axis sêê. After annealing, this ratio is reversed; the anisotropy of electrical conductivity in undoped samples and samples with different concentrations of tellurium changes its sign.
Anisotropy is also exhibited by the thermopower and Hall coefficients of samples doped with tellurium. At ~77K, in undoped samples and samples doped with 0.001 at.% tellurium and subjected to heat treatment, with increasing magnetic field strength, the anisotropy of α and RH increases (table 2). Figure 3 shows that the sensitivity of s, α and RH of tellurium-doped samples to a magnetic field also depends on heat treatment and the direction of the extrusion axis, as in undoped Bi0.85Sb0.15 samples. In bismuth and bismuth-antimony alloys, the extrema that contribute to the transport phenomena are located close to each other, and the expansion coefficients have a noticeable anisotropy [30]. It should be expected that the extrema will slightly shift relative to each other with temperature.
The experimental data obtained in tellurium-doped samples are satisfactorily explained by the change in the crystal structure of Bi0.85Sb0.15.
Antimony bismuth crystals have a layered structure and, therefore, defects formed during plastic deformation are concentrated mainly between the (111) planes of the crystals. Since, in extruded samples doped with tellurium and subjected to heat treatment, electrons scatter more strongly in the direction perpendicular to the extrusion than in the direction of the extrusion axis, the increase in mobility and electrical conductivity in the direction parallel to the extrusion axis as a result of heat treatment is greater than in the direction perpendicular to the extrusion axis. Therefore, in samples that have undergone annealing, the anisotropy s at ~77K is opposite to that of samples that have not undergone annealing.   
At 77 K, the thermal conductivity for samples doped with tellurium and heat treated in the parallel direction of the extrusion axis is greater than in the perpendicular direction (figure 3).
At ~77K, the thermal energy in the Bi0.85Sb0.15 solid solution is mainly transferred by lattice vibrations and conduction electrons [39]. Based on this, according to the expressions χl= χ-χe (1) and χe=LsТ (2), the electronic (χe) and lattice (χl) components of thermal conductivity are calculated, respectively.
Here χ is the total measured thermal conductivity, s is the electrical conductivity at a given temperature Т, L= A(k/e)2 is the Lorentz number, k is the Boltzmann constant, e is the electron charge. The value of A was estimated from the dependence of A on the thermopower coefficient [38].
Calculated electronic components of thermal conductivity χe at ~77K for undoped samples and samples doped with tellurium 0.0001; 0.0005; 0.001; 0.005 and 0.1 at.% are equal: in the parallel direction 0.10; 0.14; 0.14; 0, 11; 0.18 and 0.37, in the perpendicular direction 0.08; 0.13;0.12;0.09; 0.17 and 0.34 W/m·K, respectively.

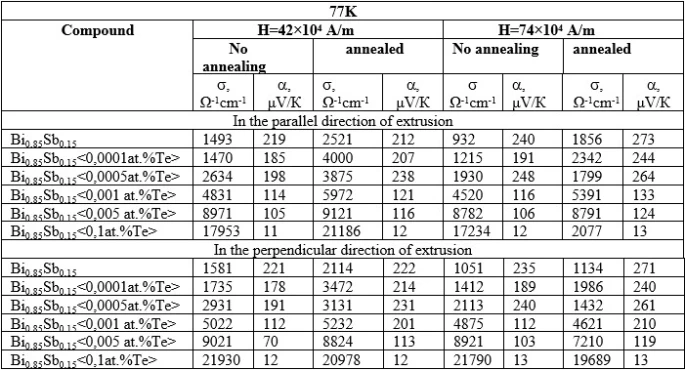
Table 2. Electrical parameters of extruded samples of the Bi0.85Sb0.15˂Te˃ solid solution at various magnetic field strengths at~ 77K

Full size image

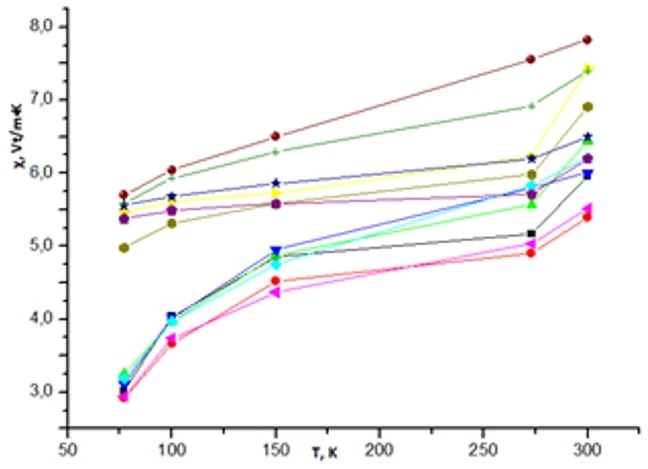
Figure 3. Dependence of thermal conductivity coefficient χ of extruded samples of Bi0.85Sb0.15 solid solution subjected to heat treatment on temperature. Designations are the same as in figure 1

Full size image

Table 3. Dependence of the coefficient of total thermal conductivity χ (W/m·K) and its electronic (χe) and lattice (χl) components in extruded samples of the Bi0.85Sb0.15˂Te˃ solid solution on the tellurium concentration in the parallel and perpendicular direction of extrusion at~ 77K

Full size image

In this case, the lattice component χl for the above samples, calculated by formula (1), is equal to: in the parallel direction 2.92; 3.11; 3.05; 5.36; 5.35 and 5.33 in the perpendicular direction 2.84; 2.98; 2.82; 4.89; 5.21 and 5.46 W/m·K, respectively (table 3).
During heat treatment, deformation defects formed during plastic deformation, which are centers for electrons, are “healed”. As a result, s of undoped Bi0.85Sb0.15 samples and tellurium-doped samples at ~77K increases strongly in the direction of the extrusion axis, and the anisotropy s changes its sign.
Note that the textures themselves and their change during deformation are completely explained by the occurrence of plastic deformation. Changes in texture depending on the degree of deformation during upsetting are explained by the fact that plastic flow in grains oriented perpendicular to the sample surface, i.e. included in the texture orientation cannot occur. Grains with other orientations are deformed and rotated, accompanied by the rotation of adjacent grains associated with them, and therefore, at low degrees of deformation, the original texture is destroyed [40,41].
In texturized polycrystals, anisotropy is related by its nature to the stacking of individual crystallites (grains) during pressing [42].
It should be noted that the unalloyed alloy, which has the highest band gap among Bi-Sb solid solutions in the temperature range 90–260 K, has a lower value of ρ than alloys with a narrower band gap [43]. This is due to the fact that in an alloy with 15 at.% antimony, an additional group of Ʃ holes takes part in the charge transfer phenomena. Antimony atoms in bismuth, being a substitutional impurity, do not have a significant effect on carrier scattering, but change the energy spectrum, thereby changing the conductivity.
When measuring galvanomagnetic coefficients in weak magnetic fields in bismuth-antimony crystals doped with tellurium donor impurities to a level where only the electrons of the L-extrema of the conduction band take part in the transfer phenomena [44].
Doping of Bi-Sb and bismuth alloys with tellurium leads to the fact that the difference in these substances, determined by the position of the extrema of the conduction and valence bands, ceases to play a role. Therefore, the electronic subsystems in these substances can be considered identical.
The magnetic field increases the resistivity of doped and undoped samples of Bi0.85Sb0.15 solid solutions. It affects the undoped and the sample doped with 0.0005 at.% Te more strongly, to a lesser extent, at higher tellurium concentrations of 0.1 at.% Te. The absolute values ​​of magnetic resistivity decrease with increasing temperature, due to an increase in the scattering of charge carriers.
The influence of the magnetic field on s of samples doped with 0.0005 at.% Te and heat treated is greater than in samples that have not been heat treated. At tellurium concentrations of 0.1 at%, the effect of heat treatment and magnetic field on s is almost absent (insignificant) (table 2).
The low magnetoresistance in unannealed and heavily doped samples compared to annealed samples and samples with a concentration of 0.0005 at.% Te is associated with structural defects. Structural defects formed during extrusion, as well as those created by tellurium impurities at high concentrations, greatly reduce the electron mobility. At low temperatures, samples of the Bi0.85Sb0.15 solid solution doped with 0.001 at.% Te are impurity semiconductors with an electronic type of conductivity. In this region, Te impurities, by creating additional electrons in the conduction band, lead to a decrease in ρ. At high temperatures (~300K), samples of the Bi0.85Sb0.15 solid solution are intrinsic semiconductors, electrons are mainly scattered by acoustic vibrations of the lattice. Therefore, at high temperatures, the effects of heat treatment, tellurium impurities, and magnetic field do not have a noticeable effect on the ρ of the samples. The change in ρ at high temperatures, at high tellurium concentrations (up to ~0.1 at.% Te) is probably due to a change in the band gap in the studied samples. However, the anisotropy of the electrical and thermal properties relative to the extrusion axis is preserved even at ~300K.

Figure 4. Dependences of electrical conductivity (a, b) and thermopower coefficients (c, d) of extruded samples of the Bi0.85Sb0.15 solid solution on the magnetic field strength; a, c - not passed, b, d - heat treated; The notation is the same as in figure 1.

a                                                                             b

Full size image

c                                                                         d

Full size image

The strong effect of tellurium impurities on the electrical and thermal properties at low temperatures can be explained by the fact that Te impurities have an “ordering” effect on the structures of Bi–Sb systems [45]. Such an effect in extruded Bi0.85Sb0.15 samples that did not undergo heat treatment, i.e. in samples with an ordered structure, it manifests itself more strongly and Te impurities in these samples play, as it were, the role of heat treatment. The decrease in the magnetoresistance in both directions of the extrusion axis in samples with a high Te concentration is caused by a decrease in the mobility of charge carriers in doped samples relative to undoped samples.  In the samples, unalloyed and not annealed, s in the absence of a magnetic field in the entire temperature range in the direction perpendicular to the extrusion axis (s^) is greater than in the direction of the extrusion axis (sêê). After heat treatment, this ratio is reversed. At low concentrations of donor tellurium atoms (up to 0.0005 at%), the anisotropy s at ~77 K without a magnetic field in samples that have not undergone heat treatment is greatly weakened. However, as the magnetic field strength increases, a strong anisotropy appears. Moreover, in all cases in a magnetic field sêê˃s^. As the tellurium concentration in the samples increases, the anisotropy s and its dependence on the magnetic field strength weaken. A similar influence of tellurium is observed in the Bi0.85Sb0.15 samples that have undergone heat treatment of the anisotropy of thermal conductivity and in the dependence χ(Н) (figure 5).

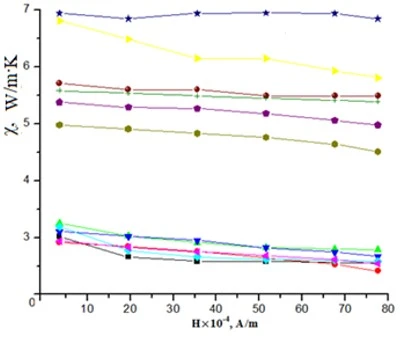
Figure 5. Dependences of the thermal conductivity coefficient χ of the extruded samples of the Bi0.85Sb0.15 solid solution that underwent heat treatment on the magnetic field strength. The designations are the same as in figure 1

Full size image

Tellurium in the amount of 0.0001 at.% practically does not change the value of α. A further increase in its concentration leads to a decrease in the absolute value of α, especially at low temperatures. In Bi0.85Sb0.15˂Te˃ alloys heavily doped with tellurium, the thermoelectric power becomes anisotropic.
The anisotropy α can be associated with the presence of several nonequivalent extrema in the conduction band or several scattering mechanisms with different relaxation time anisotropy.
The small absolute value of α under strong degeneracy, i.e. at high tellurium concentrations, only the non-parabolic zone provides if scattering occurs on acoustic phonons.
In samples containing up to 0.0005 at.% Te, heat treatment has little effect on the absolute values ​​of α in the absence of H. In unannealed and annealed samples unalloyed and doped with tellurium up to 0.005 at.%, a significant change in α under the action of a magnetic field is observed at low temperatures. In samples of Bi0.85Sb0.15 with a tellurium concentration of 0.001 at.% that underwent heat treatment, the absolute value of α in the perpendicular direction is more sensitive to the magnetic field than in the parallel direction of the extrusion axis (figure 4). In the same samples, the values ​​of thermopower anisotropy (Dα) at ​​the magnetic field strength H=42x104A/m is Dα=80 μV/K (table 2).
At high tellurium concentrations, RH of the samples is almost independent of temperature. This behavior of RH confirms the presence of a large electronic contribution to the transfer phenomenon in the Bi0.85Sb0.15 ˂Te˃ samples.
Turning to the band structure of bismuth [46] and bismuth-antimony alloys [47] one can understand the reason for the change in the anisotropy ρ with a change in the concentration of tellurium impurities. The isoenergetic surfaces of L-electrons and L-holes are similar in structure; therefore, the anisotropy of partial conductivities in an undoped alloy should be small. Doping leads to a decrease in the level of the chemical potential deep into the valence band, which leads to a change in the anisotropy ρ relative to the undoped sample.
The most reliable evidence of the prevailing role of T-holes at low temperatures is the isotropy of α under heavy doping, when the chemical potential level is deep in the valence band. As the temperature rises, the level of the chemical potential gradually rises and the degeneracy falls. In bismuth-antimony alloys, the thermopower anisotropy in the transition region is due to T-holes [48,49]. The maximum thermoelectric power in intermediate magnetic fields Δα(H) is explained by the presence of electrons of three ellipsoids in alloys and strong anisotropy of the electron spectrum, whereas for electrons of one ellipsoid, but also with strong anisotropy of the electron spectrum, a monotonic dependence on the magnetic field is theoretically obtained.
Bismuth-antimony alloys have a layered structure, so charge carriers scatter differently in different directions. Due to the fact that charge carriers scatter more strongly along cleavage planes, the anisotropy ρ changes with temperature. As the temperature increases, the carrier relaxation time decreases faster in the direction of the trigonal axis. As the temperature rises, the mean free path of charges decreases, and the effect of the anisotropy of Fermi surfaces on the anisotropy ρ of bismuth and Bi-Sb alloys at high temperatures is weakened.
Thus, the anisotropy of the electrical properties of extruded Bi0.85Sb0.15 samples is caused by texture formation along the extrusion axis during plastic deformation. In this case, the anisotropy coefficient depends on the tellurium concentration and heat treatment, which is mainly due to the change in the contribution of various charge carriers to the conductivity from the corresponding Fermi extrema.

Conclusion

It has been found that samples of Bi0.85Sb0.15 solid solution that have not undergone annealing, s, at low concentrations are more sensitive to Te impurities than samples that have undergone heat treatment. In extruded samples doped with tellurium and subjected to heat treatment, electrons scatter more strongly in the perpendicular direction of extrusion than in the direction of the extrusion axis, and during annealing, the increase in mobility, electrical conductivity and thermal conductivity in the direction parallel to the extrusion axis is greater than in the perpendicular direction. With an increase in the tellurium concentration, the influence of tellurium impurities and the magnetic field on the electrical and thermal properties of the samples that underwent and did not undergo heat treatment weakens. In extruded samples of Bi0.85Sb0.15 with 0.001 at.% Te after heat treatment, the absolute values ​​of α in the perpendicular direction of the extrusion axis are more sensitive to the magnetic field than in the parallel direction. In these samples, the values ​​of thermopower anisotropy (Dα) at ​​the magnetic field strength H=42x104A/m reaches the value Dα=80 μV/K. High mechanical strength properties and values ​​of Dα=80 μV/K make it possible to recommend this material for the creation of highly efficient anisotropic thermoelements in various energy converters.

References

About this article