Involvement of temperature dependent thermal conductivity and diffusion coefficient on bio-convective flow partial differential equations of Williamson model with radiation phenomenon

Abstract

Introduction

In 1929, Williamson presented a model that illustrated the rheological properties of non-Newtonian fluids. Ahmed et al. [1] recently used the Williamson model to investigate the behavior of these fluids and found that a stretching cylinder passes beneath the stagnation point area. They gave a thorough explanation of how various physical characteristics affect velocity profiles. Williamson fluid flow's heat transmission properties, as well as its changing heat conductivity and generation/absorption impact, were determined by Bilal et al. [2]. The Williamson model is one of these mathematical models that achieved shear thinning effects, meaning that by raising the shear rate, the fluid model's viscosity decreased. Khan et al. [3] achieved variable fluid characteristics by finding an accurate solution for the Williamson nanofluid's radiative flow across a porous surface when a porous medium is present. Microorganisms travel by a fluid dynamic process called bioconvection. Because they are much denser than water, the microorganisms swim upward in this kind of motion. Gyrotactic microorganisms, like algae, have a tendency to pierce the uppermost layer of fluid given that they swim upward. As a result, the fluid layer above becomes thicker compared to the layer below, which leads to unstable density stratification expressed by Shafiq et al. [4]. The study of nanofluids have amazing heat transit capabilities when compared to pure fluids in a variety of industrial and technical applications, there are many uses for studying nanofluid patterns with bioconvection impacts determined by Khan et al. [5]. A natural phenomenon known as "bioconvection" is created when single-celled or colony-dwelling microorganisms move randomly. Bio-convection systems are created by the directed motion of microorganisms, wherein gyrotactic microorganisms swim contrary to gravity in pure water. According to Waqas et al. [6] investigation, the upper part of the suspension has a higher density than the lower. Researchers worldwide are focusing on the diverse applications of free convection in various industrial and engineering sectors. The development of heat transfer systems is necessary to maximize thermal output efficiency, Mebarek-Oudina et al. [7] analyzed the majority of engineering operations result in high temperatures. Convective flow embedded in porous materials was used by Qasim et al. [8] in thermal exchangers, solar energy collectors, construction of buildings, extraction of oil, geothermal energy, polluted groundwater, and nuclear power plants, among various other fields of engineering. Nanoliquids provide effective methods for heat transfer. Nanofluids are proven to be advantageous in different contexts, including heat transference. To show fluid characteristics, several models of fluids have been presented across time. Cross put out a generalized Newtonian fluid model known as the Cross-viscosity model by Shi et al. [9]. Due to its numerous uses in technology and aeronautical engineering sciences, such as thermal power generation, combustion engine rotators, motorized machinery, geothermal sector, chemical reactions, healthcare equipment, and computer storage facilities, scientists have been examining the heat transfer with fluid flow throughout a rotating disc. Revealed how to solve the Navier-Stokes equations by choosing an appropriate transformation; Tassaddiq et al. [10] also introduced fluid flow across a rotating frame for the first time. Because nanofluids have extraordinary heat transit capabilities when compared to pure fluids in a variety of industrial and technical applications. The goal of Khan et al. [11] work was to look into the effects of a thin, gyrotactic needle under bioconvective micropolar nanofluid flow. It is essential to create new kinds of fluids that transport heat more efficiently because of the increasing need for emerging technologies like microelectronics, the chemical industry, and power plants. The thermal conductivity of heat-transferring liquids, which frequently have lower conductivities than solids, such as engine oil, ethylene glycol, and water, is examined in the research conducted by Hayat et al. [12]. The mathematically aspects of temperature-sensitive, thermally stratified, alterable viscosity on a nonlinear stretching sheet with Williamson nanofluid were studied by Khan et al. [13]. The relationship between the radiation of heat and thermal stratification impacts and the characteristics of tangent hyperbolic fluid flow, Rehman et al. [14] scrutinized particularly when aided via an inclined cylinder-like surface, has not been examined. One of the main obstacles to improving the efficiency and compactness of such thermal systems is the poor thermal conductivity of common heat transfer fluids, including water studied by Parvin et al. [15]. The fundamental component of many machine-made applications is the transport of heat. About the capacity of thermal devices and systems, heat transmission is dependent upon the working fluid's thermal conductivity. While Nadeem et al. [16] discovered that nanoparticles improve both the effectiveness and heat transfer of base fluids, Haq et al. [17] investigated nanofluid stagnation point flow over a stretched sheet with MHD and heating effects.
The current knowledge of mass and heat transport under various magnetic fields, as shown by flow visualization findings, Mebarek-Oudina and Bassaih [18] provides the numerical computation details required for melt convection modeling under magnetic fields that are quantitative. The effects of a magnetic field applied from the outside on tangent hyperbolic nanofluid were investigated by Ashraf et al. [19], with particular attention to the effects on heat radiation and thermal conductivity of the material. The effect of bioconvective micropolar nanofluid flow over a fine thread composed of gyrotactic microbes was examined by Khan et al. [20], taking into account Arrhenius stimulation energy, viscous dispersal, and distinct chemical processes. The homotopy evaluation method is used to transform the governing equations into a dimensionless arrangement. Recently, there has been debate about bioconvection in several biotechnological domains where fluids and their physical characteristics are essential. Heat and mass transfer utilized by blended nanofluids result in an event known as bioconvection. In order to transfer a binary fluid over a multilayered stretching surface, Dawar et al. [21] proposed an empirical study of a 2D, electrically conducting, magnetized vulnerable fluid that contains nanoparticles and gyrotactic microbes. In this work, Hayat et al. [22] study the unsteady 2D boundary layer flow of an inert Williamson fluid over a volatile porous stretched surface with thermal radiation. Impacts of electric and magnetic fields are taken into account. The work emphasizes the impacts of heat emission that is not linear and a uniform magnetic field. The homotopy analysis approach and the ND-Solve methodology were used to convert and solve the governing equations. A comparison is made between the numerical and analytical findings both visually and numerically, and good agreement was found by Shah et al. [23]. The improved control of producing entropy in the flow of a non-Newtonian fluid (Williamson fluid) toward a smooth and stretchable exterior is the subject of investigations by Qayyum et al. [24]. The subject of the Qasim et al. [25] inquiry is MHD peristaltic flow within wavy fences in an asymmetrical pathway, in which the boundary layers move at the speed of peristaltic waves in conjunction the entire channel's length. The electrical conductivity in both the Joule heating and Lorentz force is assumed to be temperature-dependent during this inquiry. By reducing regulating PDEs to connected nonlinear ODEs, magnetic field hydrodynamics (MHD) studies magnetic and velocity components in the context of an electrically-conductive fluid. Such a flowing fluid can experience currents being induced by the magnetic field, which generates forces that alter the magnetic field itself and the fluid. Shoaib et al. [26] studied the overall MHD incidence described by a system of differential equations made up of Maxwell's equations and Navier-Stokes equations. In many technical and industrial operations, such as melt spinning, hydroelectric power plants, plastic film manufacture, nuclear power plants, and so on, the magnetohydrodynamic movement of viscous fluid is crucial expressed by Khan et al. [27]. The effects of chemically reactive substances and combined convection on MHD Williamson nanofluid were studied by Khan et al. [28]. The work of Chamkha et al. [29] concentrated on convective boundary-layer circulation across a non-isothermal slide under stable state hydromagnetic driving. Hydrodynamics in the context of a magnetic field was shown by Rizwana et al. [30].  Analysis is done on heat transport in unstable non-Newtonian fluid flow, where fluctuations flow is controlled by magnetohydrodynamics and thermal conduction is enhanced by nanoparticles.
In viscous and chemically responsive nanofluid dynamics in a medium that is porous, Rasool et al. [31] investigated the characteristics of the Cattaneo-Christov model with particular emphasis on expanding velocity on the solid/sheet surface as well as stream velocity at the surface that is unbound. Khan et al. [32] explored that the ordinary differential system is developed by appropriate transformations. We used the Optimal Homotopy Analysis Technique (OHAM) to create a convergent series solution. Williamson (1929) created this model, which was later used by a few researchers to investigate fluid flow by solving the Williamson nanofluid flow regulating system investigated by Raza et al. [33]. Equations pertaining to the momentum, energy, concentration, and density of the microorganisms are reduced to non-linear ordinary differential structures through the application of comparable transformations. The OHAM-BVPh2.0 package is used to code the derived equations in the Mathematica software. The influence of many physical characteristics is the investigation's most significant finding. The average residual error is organized for temperature, concentration, density of microorganisms and velocity using the OHAM. A visual discussion of the skin friction coefficient, temperature gradient, and mass transfer rate is provided. Optimum homotopy analysis (OHAM), a semi-analytical technique, has been employed to create answers for the suggested mathematical model. The impact of a thermophoretic velocity and slanted magnetic field on flow and heat-mass transmit throughout mass suction/injection using OHAM is investigated in this study [34- 40].
The literature research points out that the mentioned features have not yet been the subject of any investigations. Very little research has been done using this strategy. With the inclusion of a magnetic field, thermal radiation, variable thermal conductivity, variable diffusion coefficient, heat generation, and a density of microorganisms across a stretched sheet, the current model is designed to be a complicated one. The division of the current project is shown as: The model's formulation is covered in Section-II. In Section-III, physical quantities are covered. Section-IV uses a numerical technique, while Section-V is based on an examination of the data. The main points are covered in Section-VI.

Formulation

This article examines the activation energy feature for a Williamson nanofluid flowing steadily and incompressibly across a nonlinear stretching plate in two dimensions (2D). Let the plate be extending along the ӽ  coordinate at certain velocity of Bӽ13 , the flow of nanofluid is normal to the ӳ  coordinate (refer to figure 1). The magnetic field B=Boӽ-13  is assumed to be normal to the fluid flow. Additionally, it is thought that at the surface, Uw  denotes velocity, Ŧw  represents temperature, and concentration is given by Ċw ; Ŧ∞  and Ċ∞  respectively represent temperature and concentration at infinity. Provided below are the leading equations.
The expression for the Cauchy stress tensor is:

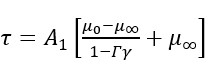              (1)

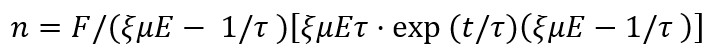(2)

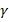 is symbolized as

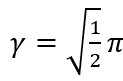    (3)

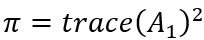(4)

{figure: 1472}

In this case, 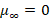 and 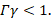 Equation (2) so decreases as

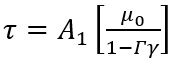(5)

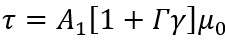    (6)

The dominant equations under these particular circumstances are:
Continuity equation

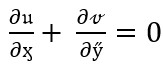(7)

Equation of Momentum

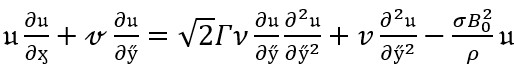(8)

Using the boundary conditions

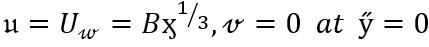   (9)

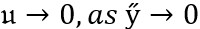                              (10)

We use transformations [41]:

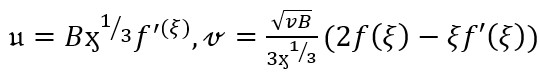(11)

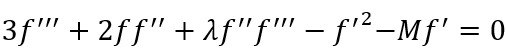  (12)

Equations (8-10) are simplified using equations (11-12) as follows:

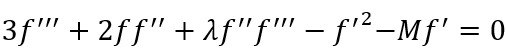  (13)

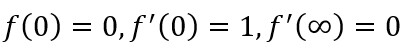    (14)

Energy equation

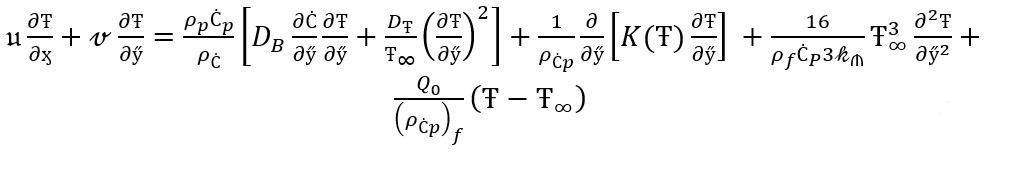(15)

Using the boundary conditions

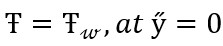                                               (16)

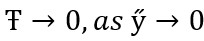                   (17)

Equations (11-12) and (15-17) are simplified as follows:

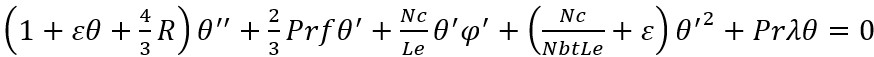(18)

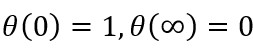                                           (19)

Concentration equation

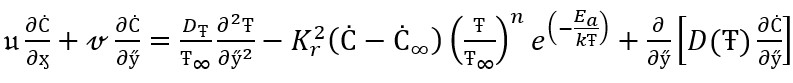(20)

Using the boundary conditions

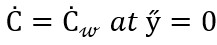       (21)

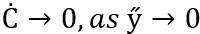   (22)

Equations (20-22) are simplified using equations (11-12) as follows:

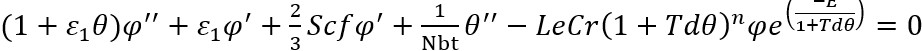  (23)

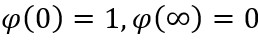        (24)

Density of Microorganisms equation

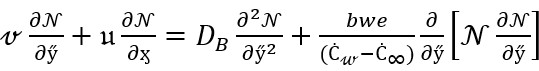   (25)

Using the boundary conditions

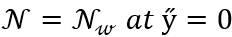   (26)

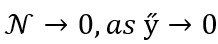 (27)

Equations (11-12) are used to decrease equations (25-27) in the following way:

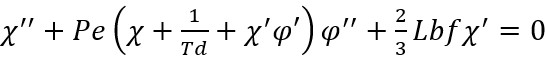 (28)

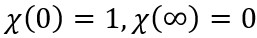    (29)

One way to represent these parameters is as follows:

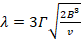 stands for the Williamson parameter, 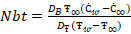 symbolizes the various diffusivity,  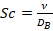is the Schmidt number,  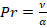 is the Prandtl number ,  indicates the Lewis number ,  represents the ratio of heat capacity,   symbolize the rate of reaction , 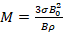  denotes the magnetic parameter,  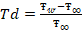  is the difference of temperature,  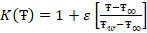denotes variable thermal conductivity, and  stands for variable diffusion coefficient.

Physical quantities

The rates for heat and mass transfer, as well as non-dimensional versions of surface drag coefficients, are:

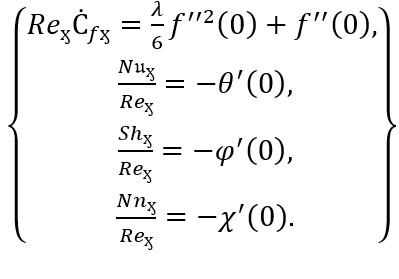(30)

 

Solution by OHAM

For OHAM solutions, suitable starting deformations and auxiliary operators are:

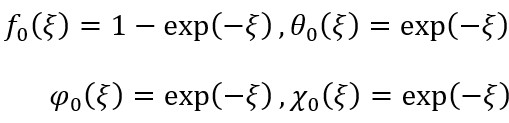(31)

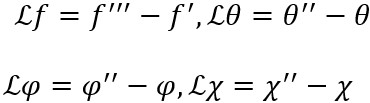   (32)

The linear operators listed above follow.

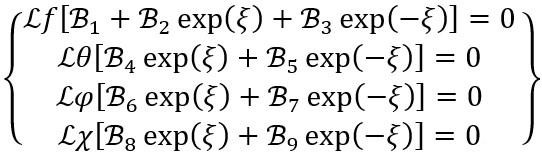(33)

Where  displays the random constants.

Result and discussion

Utilizing boundary conditions (14), (19), (24), and (29), respectively, the Williamson nanofluid flow across a nonlinear expanding sheet's equations (13), (18), (23), and (28) are systematically solved using OHAM.

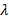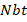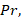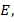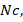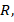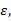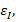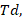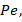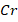Williamson parameter , magnetic parameter , diffusivity parameter , Prandtl number  Lewis number  Schmidt number , activation energy parameter  heat capacity ratio  Radiation parameter  Variable thermal conductivity  Variable diffusion coefficient  Temperature difference  Peclet number  Bioconvection Lewis nmber  and reaction rate  are some of the resultant parameters that physically illustrate variation in the Williamson nanofluid flow. The velocity profile fluctuation across Williamson and magnetic parameters is shown in figures 2a, b. Increases in the magnetic parameter values result in a reduction of the velocity profile (see figure 2a). Precisely speaking, a rise in the magnetic parameter diminishes the fluid flow's mobility since it physically causes the Lorentz force to be generated, and that consequently gives the particles in the fluid resistance to movement. So,

{figure: 1476}

The velocity profile drops as one increases the magnetic factor. Figure 2b illustrates how the velocity profile reduce with greater numbers of the Williamson parameter. The Williamson parameter measures the relaxation to delays time ratio. Facilitating relaxation is what allows fluid particles to return to their original positions. In conclusion, when a fluid's viscosity increases, its velocity decreases. The temperature distribution is plotted against two different estimates of the radiation parameter and the variable thermal conductivity parameter, respectively, in figures 3a and 3b. The temperature sketch increases in proximity to the stretched surface as variable thermal conductivity increases. In terms of the physical process of heat transmission, thermal radiation is essential. Figure 4a illustrates how the thermal profile varies as a function of the Prandtl number. A higher Prandtl number causes the fluid's flow to be resisted by more intense kinematic viscosity than density, which lowers the distribution of temperatures and reduces the boundary layer of heat. The thicker nanofluid caused by this phenomenon shows a decrease in the thermal profile. Figure 4b provides an illustration of the thermal profile variations using the heat capacity ratio. A higher wall temperature and a higher thermal profile are the physical results of raising the heat capacity ratio parameter. In addition, the boundary layer's thickness decreases in this situation. The thermal profile fluctuates according to the diffusivity ratio, as shown in figure 4c, and the profile gets smaller when the diffusivity value increases.

Higher values indicate a decrease in boundary layer width owing to reduced temperature and concentration narratives. Figures 5a and 5b show Lewis number swings in temperature and concentration curves. The physical relationship between the Lewis number and the nanofluid's thermal diffusivity ensures that the Brownian diffusivity remains constant.

Figure 6a, 6b, and 6c show the fluctuation in the concentration profile, variable diffusivity, rate of reaction, and Schmidt number. As seen in figure 6a, a rise in 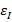 induces a decrement in the mass diffusivity of the fluid, resulting in a thinner mass boundary layer. When the Schmidt number rises, the concentration profile simplifies (see figure 6b). This is because it would rise as a result of the momentum diffusivity consequences, but it would also diminish the impact of the mass transfer rate, leading to a lower concentration profile. Higher response rate values cause the concentration profile to rise (see figure 6c). In actuality, usage of reactive species rapidly declines with increasing reaction rate.

The motility distribution grows together with the Peclet factor 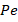 (figure 7a). The density of microorganisms in the existence and shortage of a magnetic field is depicted in figure 7b, where a reduction in the microbial population curves is indicated by increased temperature differential parameters. Figure 7c shows that when the bioconvection Lewis numbers  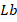value increases, the motile microorganisms profile decreases.

Table 1 represents individualized squared residual error utilizing the most accurate auxiliary variable data. The impacts on the skin friction coefficient are shown in table 2. Table 3 displays the heat transfer rate versus a number of relevant factors to highlight their importance. Table 4 shows the parameters disparity effect on concentration profile. Table 5 shows that the density of organism’s number 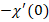 rises with rising  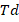and 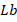 values and falls with growing  values.

Conclusion

Utilizing OHAM, the paper examines the activation energy characteristic of a 2D steady, incompressible boundary layer flow of a Williamson nanofluid across a non-linear stretching plate. A visual representation of the changes in fluid flow caused by embedded parameters is shown. The following list contains the primary points of the current analysis: Increasing the magnetic and Williamson parameters causes the velocity profile to decrease; As the diffusivity parameter and Lewis numbers increase, the temperature function becomes less severe; however, the opposite effect is seen when the heat capacity ratio increases; The concentration function decreases as the reaction rate, Lewis number, and Schmidt number increase; Heat transmission rate increases with increasing Prandtl number; The motility distribution grows together with the Peclet factor ; It is thought that decreasing microorganism curves are indicated by larger values of the temperature differential parameter 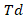; As the bioconvection Lewis numbers  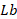value increases, the motile microorganisms profile decreases.

References

About this article