Utilization of OHAM on mixed convective flow of Williamson fluid model with viscous dissipation over a stretched cylinder

Abstract

Introduction

The study of magnetohydrodynamics, which examines the magnetic characteristics of materials that are electrically conductive, has found use in many industrial, scientific, and technological fields. Examples of these include the manufacture of chemicals, liquid metals, electronic chip cooling, plasma, electrolytes, heat extraction from nuclear power plants, and saltwater examined by Reddy et al. [1]. An examination of the outcomes of magnetohydrodynamics on the rotational flow of Casson Carreau nanofluids is taken into consideration. Brownian motion, Thermophoresis and heat source exhibit a mutual correlation with the distribution of temperature. Arrhenius activation energy is used to study the diffusion of chemically reactive species studied by Ali et al. [2]. Magnetohydrodynamics pertains to the examination of the magnetic characteristics of fluids that possess electrical conductivity. Such magnetic fluids include salt water, liquid metals, plasmas, and electrolytes explored by Shah et al. [3]. A boundary layer flow across a decreasing surface occurs in several technological processes. Such circumstances arise in a variety of industries, including the processing of polymers, the fabrication of glass sheets, paper, textiles, and many more addressed by Nadeem et al. [4]. In engineering and technology, the existence of two-phase motion in magnetohydrodynamics within the confined region between two parallel plates holds significant importance. Two-phase motion is seen in chemical production in agitated vessels, spray and sparkle columns, load columns, gas-liquid coatings, fabrication, and heat exchange equipment researched by Shehzad et al. [5]. Due to its importance in industrial and architectural applications, the phenomenon referred to as mixed convection also acknowledged as coupled free and forced convection has attracted a lot of interest. The most famous uses of this phenomenon may be found in various disciplines, including building design, optical manufacturing, heat transfer in solar collectors, nuclear reactors, furnaces, electronics cooling, and food processing analyzed by Mebarek-Oudina [6]. Because of its wide range of applications, there has been an exploration of mixed convection flows that encompass both heat and mass transfer, with the additional consideration of Arrhenius activation energy and chemical processes. The quality of the majority of products and industrial is dictated through chemical reactions and cooling rates, which can be either connected to type or reaction delved by Sharma et al. [7]. Through an upright cylinder, the consequences of heat radiation on mixed convective boundary-layer flow are investigated concerning Lorentz's forces. In addition, the form factor is evaluated by Chu et al. [8]. This article focuses on the combined convection, mass and heat transfer properties of a chemically reactive species-containing a plate and a cone covered in Eyring-Powell nanofluid inspected by Khan et al. [9]. Under different temperature conditions, the study outlines an irregular and incompressible Williamson nano-liquid flow driven by a porous stretching cylinder. Based on the impact of a heat source or sink that is not uniform, mixed convection on flow and heat transmission, the flow field experiment is set up by Song et al. [10]. Investigations are conducted on mixed convection, gyrotactic microorganisms and nanoparticles coexist on a convectively heated vertical surface gravitationally driven non-Newtonian nanofluid sheets. The liquid film flow is conducted utilizing boundary conditions specified by the aggressively organized nanofluid model scrutinized by Khan et al. [11]. Heat transport over a stretching cylinder and Williamson fluid flow are examined. It is expected that the thermal conductivity changes according to temperature. The study appropriately accounts for the effects of generating heat and absorption discussed by Malik et al. [12]. Concerning heat generation and absorption as well as viscous dissipation, this study aims to examine the 2D Casson hybrid nanofluid flow thru a nonlinear expanded surface beneath the influence of a magnetic field. Enhancing the heat transfer relationship is the main objective of this research inquired by Hameed et al. [13], as it is highly sought after in the engineering and manufacturing sectors. Many industrial operations, such as the production of paper, energy, electronic device cooling, and cooling of atomic reactors, depend on heat transmission. Girish et al. [14] studied to maximize the efficiency of the equipment, it is necessary to minimize the heat generated. For an exothermic reaction, the implications of heat generation are considered by Khan et al. [15]. Nanoparticles improve the heat transport phenomenon in the boundary layer area. Convective boundary conditions have been used in the investigation of mass and heat transfer. The variables that are independent in governing equations are decreased with the use of appropriate dimensionless variables studied by Khan et al. [16]. Rasool et al. [17] scrutinized the effect of viscous dissipation across a porous decreasing sheet, Joule heating, and the steady flow of magnetohydrodynamics of water nanofluids. The primary focus of Khashi'ie et al. [18] is the examination of MHD hybrid nanofluid flow accompanied by heat transfer on a mobile plate, with particular emphasis on the incorporation of Joule heating effects. Sohail et al. [19] expressed the consideration of radiation and Joule heating affects important, entropy production, thermal propagation and species on Casson liquid boundary layer flow on a surface that is linearly elongating.  Additionally, entropy analysis is considered for an in-depth investigation of irreversibility inspected by Zidan et al. [20]. Examining the objective of this analysis is to scrutinize entropy generation in a pseudoplastic Williamson nanofluid flowing in an angled magnetic field, while gyrotactic motile microbes move over a cylinder that is in motion investigated by Naz et al. [21].
Magnetohydrodynamics finds many practical uses in engineering and technology, such as electromagnetic casting, magnetohydrodynamic sensors, magnetic drug targeting, liquid-metal cooling of reactors, and plasma and crystal formation. The magnetic inductions' strength determines the behavior of magnetohydrodynamics. The current's Hall influence is not able to be disregarded as the magnetic force increases explored by Shah et al. [22]. Effects of hydromagnetic forces on electrically conducting viscous fluids are widely used in a variety of scientific procedures, including plasma confinement, MHD generators, electromagnetic pumps, metallurgical processes, and MHD propulsion systems delved by Sahoo and Nandkeolyar [23]. In this paper, the thermal effect of rotating and bidirectionally stretching cylinders generating a Maxwell nanofluid spinning motion mixed convection flow is analyzed by Islam et al. [24]. The current analysis also considers the results of internal heat sources and Joule heating. In addition, the flow is subjected to a homogeneous magnetic field under convective boundary conditions. We report the dependence of skin friction coefficients, local Sherwood number, and local Nusselt number on relevant properties such as chemical reaction, and heat production. To explain the unique characteristics of the solutions, these effects are presented by Saleem et al. [25] both visually and tabulatorily. For the reasons mentioned above, this work undertakes a novel visualization of the impacts that result from viscous dissipation, velocity slip, and nonuniform heat generation/absorption in the context of a viscoelastic fluid's heat transfer flow. Rasheed et al. [26] analysis concentrates on the results that arise from a stretched surface that is enmeshed in a porous media. Zaib et al. [27] investigated the relationship between the properties of entropy production and the significant effects of viscous dissipation and Joule heating in the mixed convective incompressible flow of a tangential hyperbolic magnetite iron oxide nanofluid. A magnetic field and heat radiation induce this flow down an inclined impermeable plate. Blood is considered to be a non-Newtonian fundamental fluid in this paradigm. We have generalized the non-Newtonian Darcy-Forchheimer MHD flow over an incompressible stretched surface in the incidence of reactive chemical species. Under entropy generation, the chemically reactive species and Darcy Forchheimer influence are taken into account. Engineering processes have primarily used entropy generation analysis to enhance theoretical and mathematical assessment problems studied by Khan et al. [28]. In industrial, engineering, and thermal polymer processing operations, the dynamics of the entropy production phenomenon are significant. Researcher's primary goal is to lessen the creation of entropy to improve industrial system's thermal efficiency scrutinized by Wang et al. [29]. The rate of entropy generation for nanofluid in a whirling MHD flow in the manifestation of thermal radiation and the Joule heating effect has been examined by Khan et al. [30]. The BVPH2.0 approach was used in this study to numerically solve the modeled issue.  The two-dimensional time-independent flow is said to be initiated by a vertical stretchy sheet. The relevant problem governing equations takes into account the formulation of the consequences of viscous dissipation and Joule heating. The nonlinear configuration of ODEs is constructed by a suitable approach in the system of PDE similarity transformations delved by Ishtiaq et al. [31]. With the aid of the Eckert number, the impact of Joule heating on nuclear and geophysical engineering flows significance is typically characterized by Ahmad et al. [32]. This includes determining the bearing of Joule heating and Hall current in the thermally radiative flow of magneto-ferrofluid while taking nanomaterials into account in heat transfer analysis. 
The nonlinear system of ODEs might be created by applying the proper similarity transformations. The homotopy analysis approach is used to solve the modelled system of equations analytically. Additionally, a HAM convergence analysis is provided by Dawar et al. [33]. Based on the HAM, the Mathematica package BVPh2.0 is used to solve the nonlinear ODEs analytically studied by Ellahi et al. [34]. The dimensionless equations are determined using the OHAM. Graphs and tables are employed to demonstrate the impact of relevant factors on streamlines, velocity, concentration, and temperature. Sherwood number, Nusselt number, and skin friction numerical values are given in a table for the modifications of various factors analyzed by Basha et al. [35]. Using the Mathematica program BVPh2.0 Software, the improved model is estimated using the well-known OHAM technique. Graphical and computational analyses have been carried out for several dimensionless parameters introduced by Waseem et al. [36]. The formulated boundary value problem can be solved using the OHAM analysis, yielding analytical results studied by Khan et al. [37]. Similarity transformations are engaged to turn the governing (PDEs) into (ODEs). The optimal homotopy analysis scheme is utilized to attain the desired outcomes. The model's optimum residual errors and convergence were calculated by Rasool et al. [38] to preserve its validity.
In-depth investigations of mass and heat transfer have not yet been carried out in the corpus of current research, especially when it comes to density of organisms, heat production, joule heating, mixed convection, and MHD for stretched flow of Williamson fluids. The purpose of this study is to close this information gap. This investigation is organized as follows:
•A thorough overview of the body of research on the transfer of mass and heat is provided in Segment-I.
•Section-II is devoted to dimensionless analysis and problem framing.
•Section-III provides further details on the ideal homotopic technique that is used to solve the resulting nonlinear model.
•Part-IV explores the physical phenomena that underlie the outcomes.
•The study's results are presented in Section-V.

Problem formulation

The investigation addresses the steady, 2-D boundary layer flow of a Williamson fluid next to a stretching cylinder that is incompressible and axisymmetric and. The analysis the relationship between heat generation and absorption and a magnetic field. The horizontal and components of radial velocity are designated as u and v. Additionally, the study accounts for the effects of viscous dissipation and Joule heating. Figure 1 illustrates the schematic representation of the fluid flow scenario under consideration. The governing equations governing this flow are articulated as follows:
Equation of continuity:

   (1)

Equation of momentum:

             (2)

Equation of energy:

                  (3)

Equation of Concentration:

           (4)

For Williamson fluid, the rheological equations are as follows.

               (5)

The definition of the extra shear tensor is,

In the given context, let 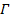 denote a positive constant . The parameters  and 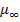 represent the viscosities corresponding to shear rates of zero and infinite, correspondingly.

In the current investigation, we have stipulated 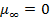under the constraint of 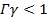. As a consequence, the expression governing the extra stress tensor is transformed into . Additionally,

                  (6)

The components of the three governing equations for the Williamson fluid that consider the impact of boundary layer effects in the cylindrical coordinate system, are explicitly delineated by Kumar et al. [39].

        (7)

     (8)

   (9)

        (10)

along the appropriate boundary conditions:

   (11)

Utilizing transformations of similarity,

  (12)

The governing equations change into the following non-dimensional versions where   :

(13)

(14)

                               (15)

under the corresponding boundary conditions:

    (16)

The following is the first order estimate for  and .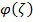

Additionally, the following definitions apply to the skin friction coefficient, Sherwood number, and local Nusselt numbers.

   (17)

   (18)

     (19)

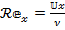 denotes the Reynolds number.

Solution through OHAM

This study employs an optimal approach to compute solutions for a coupled nonlinear system of governing differential equations. Utilizing the homotopy analysis scheme, a parameter-independent and discretization-free method, we overcome stability issues associated with numerical approaches. The scheme necessitates the careful selection of a linear operator and an initial guess, ensuring compatibility with prescribed boundary conditions. This meticulous parameter choice enhances the accuracy and efficacy of the computational results.

  (21)

   (22)

The linear operators corresponding to this context are as follows:

   (23)

These linear operators adhere to the following characteristics:

    (24)

These are subjective constants, where * with .

Entropy generation

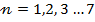The model presented encapsulates the entropy generation rate in the case of transitory axisymmetric flow of a Williamson nanofluid under the influence of nonlinear radiation.

    (25)

The characteristics of entropy generation are delineated as followsTop of Form.

          (26)

By utilizing equation (12), it is possible to express the dimensionless form of entropy generation.

(27)

Where,

          (28)

Results and discussion

Williamson fluid flow over a permeable stretched cylinder has been the subject of numerical analysis examining the implications of joule heating, mixed convection, and heat generation. This investigation systematically explores the significance of important parameters on temperature and velocity distributions, including the Eckert number , Prandtl number   suction parameter 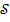, mixed convection parameter  heat source parameter , and magnetic field parameter . Additionally, the study includes the determination of the Nusselt number and skin friction coefficient to offer a comprehensive comprehension of the rates of heat transport and shear stress, respectively.

Figure 2 illustrates the alteration in the velocity profile, denoted as attributed to variations in the curvature parameter, denoted as . The velocity profile  indicates a diminishing inclination in response to the escalation of the curvature parameter 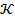. This is attributed to the augmented curvature parameter K  resulting in a reduction of the radius of curvature, subsequently leading to a diminution in resistance to fluid flow. Consequently, the boundary layer thickness experiences a reduction as the curvature parameter 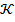 rises. Figure 3 illustrates the diminution of both the velocity gradient  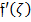and the thickness of the momentum layer with increasing . This behavior is attributed to the direct and inverse relationships that  maintains with relaxation time and specific process time, respectively. An elevation in δ corresponds to an augmentation in relaxation time, resulting in an increased resistance of the fluid. Hence, the fluid velocity and the thickness of the momentum layer undergo a reduction. Figure 4 presents the impact of the velocity distribution function's parameter for, 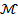. In this context, all the others pertinent physical parameters are held constant, with the sole variable being the magnetic field parameter. It is noteworthy that an augmentation in the  induces a reduction in velocity of a fluid. This phenomenon can be attributed to the proportional growth of the Lorentz force corresponding to the rise in the magnetic field . The heightened Lorentz force exerts a resisting influence on the fluid particles' movement across the surface, resulting in a decrease in their velocity. This outcome is more pronounced for planar geometrical surfaces and exhibits comparatively lower influence on cylindrical surfaces. Figure 5 depicts the influence of the 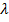 on the fluid particle velocity The velocity profiles exhibit an amplification with increasing values of the mixed convection parameter due to the substantial magnitude of the buoyancy force. Figure 6 elucidates the variation in the mixed convection parameter against the velocity gradient 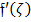. The velocity gradient 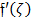experiences an augmentation in the presence of higher values of 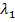. Since  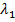encapsulates relaxation and retardation times, an elevation in  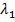results in an expanded relaxation time. This extended relaxation time contributes to heightened resistance to the movement of the liquid. The influence of the coefficient of thermal expansion , regarding the fluid velocity  is displayed in figure 7. The conditions for this investigation include  and . Figure 8 presents the velocity 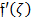 as a function of 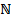, and it is evident that the baseline velocity, denoted as , exhibits an increment with an increase in . This behavior is attributed to the escalating buoyancy forces, where  represents the ratio of concentration to thermal buoyancy forces. The augmentation in N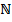  leads to a heightened velocity field. The influence of the coefficient of solutal expansion , concerning the fluid velocity 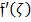, is demonstrated in figure 9. The specified conditions for this examination include  and . Figure 10 portrays the influence of the Prandtl number 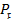 on the temperature distribution across both planar and cylindrical surfaces. It is evident that an elevation in the Prandtl number corresponds to a reduction in temperature. Within the realm of the Prandtl number  and heat transfer serves as a pivotal parameter distinguishing from thermal diffusivity to momentum diffusivity. In the thermal transfer process, reduce Prandtl values imply that heat conduction predominates over convection, whereas bigger values indicate the opposite. Figure 11 illustrates the manifestation of an exothermic reaction. An exothermic reaction characterizes a chemical process wherein energy is liberated in the form of heat. As  experiences an augmentation, the exothermic reaction becomes pronounced, leading the temperature profiles reduced. Figure 12 depicts the temperature profile for various δ values under the conditions of  and 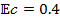. The variation of the Eckert number  against θ is seen in figure 13. In this case, increasing 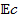 results in improvements to both θ and the corresponding layer thickness. Specifically, as  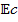is incremented, the liquid viscosity extracts energy from the fluid motion and transforms it into internal energy, consequently elevating the temperature of the liquid. Figure 14 illustrates the impact of the magnetic field parameter on the temperature profile distribution. It is observed that an augmentation in  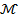introduces resistance to the motion of fluid particles through the induction of Lorentz force. Consequently, this resistance leads to the generation of internal heat among fluid particles, resulting in an overall increase in temperature. We plot concentration patterns for a range of Lewis number  values in figure 15. The ratio of the characteristic length for heat diffusivity to mass diffusivity is known as . Figures 16 and 17 show the effects of the parameters 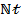 (thermal buoyancy parameter) and  (Brownian motion parameter) on the variable 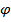. Notably, an enhancement in  is discerned with increasing , signifying a greater thermophoretic force. This force tends to relocate nanoparticles from regions of higher to lower temperature, thereby elevating 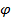. Conversely, the inverse trend is observed for 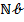, where an escalation in its magnitude intensifies the random velocities at which nanoparticles traverse, owing to Brownian effects. Consequently, an elevated results in a reduction in both 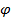 and the corresponding thickness of the concentration layer.

 Figures 18-21 elucidate the dependency of entropy generation on various parameters, including the dimensionless temperature difference 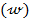, Brinkman number , 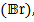 diffusion parameter ,  and magnetic field parameter 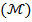, within a technical and academic context. Analysis of figures 18 and 19 reveals that the entropy profile exhibits an accelerated trend with a raise in either Brinkman number or dimensionless temperature difference. This acceleration is attributed to the augmented entropy generation resulting from irreversible mechanisms, causing an upsurge with growing . Notably, heightened values in entropy generation, arising from the irreversibility associated with fluid friction, manifest due to an augmentation in . Figure 20 presents a noteworthy observation, indicating that the entropy profile initially exhibits a decremental trend with an increasing diffusion parameter 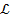, followed by an ascension after reaching a specific value of 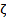. The profile of entropy generation is, as expected, more prominent for non-Newtonian fluids than for Newtonian fluids. In figure 21, the impact of the magnetic field parameter 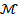on the entropy generation  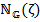is portrayed. It is evident that    experiences a decline for larger values of . This underscores the influence of the magnetic field parameter on mitigating entropy generation within the system.

Table 1 presents an analysis of the impact on skin friction coefficient   expressed as 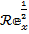 for various operational parameters, namely 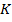, , , ,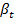  and . The observed trends indicate that an increase in the magnitudes of 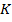,  and 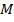 outcomes in a corresponding augmentation of the Skin friction . Conversely, variations in,  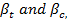 lead to a reduction in 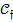. The table provides a comprehensive overview of the intricate relationships between these parameters and their consequential effects regarding the skin's friction coefficient in the context of 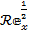. This analysis contributes valuable insights for academic and technical considerations in fluid dynamics research. Tables 2 and 3 provides numerical values for the Nusselt number  and Sherwood number 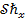, both expressed as . An examination of table 2 reveals that the heat flux, represented by , experiences a decrease with increasing values of parameters  ,  , and . Conversely, an augmentation in heat flux is observed when parameters , , and 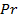 are increased. Moving on to table 3, the mass flux  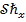demonstrates an upward trend with increased values of  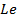and . In contrast, an increase in mass flux is observed when parameters , , and  experience an increase. These findings, as detailed in tables 2 and 3, contribute valuable insights into the interdependencies between various parameters and their impact on heat and mass transfer phenomena, making them pertinent for academic discourse in fluid dynamics research.

Conclusion

Numerical simulations were carried to investigate over a permeable stretched cylinder, the magnetohydrodynamic Williamson fluid flow, incorporating viscous dissipation along with Joule heating, mixed convection, and heat generation/absorption effects. The research yields several noteworthy decisions: The fluid temperature demonstrates an ascending trend in response to the magnetic field parameter, while the fluid velocity demonstrates a diminishing inclination concerning the magnetic field parameter; The suction parameter that improves the velocity profile is discovered, but display a diminishing effect on the fluid temperature; The fluid velocity experiences an increasing trend with the mixed convection parameter, while the temperature profile shows a declining trend; The fluid's temperature profile exhibits an inclination towards growth with respect to the heat source parameter and Eckert number; The temperature of the fluid exhibits a reducing trend concerning the 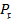; The coefficient of skin friction exhibits a negative association with the parameter for Williamson fluid but displays an encouraging perform concerning the Prandtl number and magnetic field; The Nusselt number  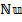demonstrates a rising behavior with the  but exhibits the reverse relationship with the 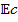. These findings contribute valuable insights into the complex interplay of parameters governing MHD Heat transmission and Williamson fluid dynamics across a permeable stretched cylinder.

Nomenclature

	Magnetic field
	Prandtl number
	Velocity components
	Extreme temperature
	Reynolds number
	External heat
	Pressure
	Ratio of concentration to thermal buoyancy
	Radius of cylinder
	Magnetic field parameter
	Curvature parameter
	Grassohf number
	Specific heat capacity
	Identity vector
	Length
	Nusselt number
	Suction parameter
	Surface temperature
	Free stream velocity
	Grashof number for concentration buoyancy
	Nonlinear thermal convection variables
	Linear and Nonlinear thermal expansion coefficients
	Linear and Nonlinear concentration expansion coefficients

Greek symbols

	Mixed convection parameter
	Thermal diffusivity
	Extra shear tensor
	Stream function
	Williamson fluid parameter
	Dynamic viscosity at zero shear rate
	Kinematic viscosity
	Fluid density
	Dynamic viscosity
	Heat source/sink parameter
	Dynamic viscosity at infinite shear rate
	Time constant

 

References

About this article