Features of the optical properties of chalcogenide glassy semiconductor Ge-As-Se(Te) systems

Abstract

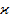In this work were determined the optical band gap (Eg), packing coefficient (  ) and average atomic volume   by conducting experiments to measure the optical transmission spectra and density ( ) of chalcogenide glassy semiconductors of Ge-As-Se(Te) systems. Reasons of changes occurring in the band gap and in the structure of the amorphous matrix of the studied materials were suggested taking into account existing ideas about the nature of the band energy spectrum of chalcogenide glasses and analysis of experimental data. The dependence of ϰ and  on Z and R are investigated for stoichiometric compositions of  and the nature of these dependencies were explained in detail.

Introduction

Chalcogenide glasses are distinguished by high transparency in the infrared (IR) region of the spectrum, a high refractive index, high optical nonlinearity, the possession of a reversible transition between states of high and low resistance values under the influence of electric field. These materials are promising for use in optoelectronics, fiber optics, nonlinear optical systems and memory devices [1- 7]. It is possible to influence the macroscopic properties of chalcogenide glass materials by changing the chemical composition or introducing an impurity, which makes it possible to expand their areas of application, as well as improve the parameters of existing devices [8, 9]. So, it is considered a reasonable approach to look for correlations between macroscopic properties and local structure, i.e. to clarify the role of local structure in controlling the electronic properties of chalcogenide glasses due to the lack of long-range order in the arrangement of atoms and the existence of ordering in regions covering closely spaced atoms. One of the main parameters characterizing short-range order in the arrangement of atoms is the average coordination number, a change in which leads to threshold changes in both structure and physical properties [10- 14]. The results of local structure studies on the short- and medium range order by conducting experiments on X-ray diffraction, Raman scattering, as well as measuring the density of the CGS of As-Ge-Se(Te) systems [14- 16] are interpreted in the framework of the void-cluster model [17] taking into account the basic principles of the chemical bond approach model (CBA) [18- 20]. An analysis of experimental facts have been shown that the local structure parameters and  density of the substance, the average atomic volume, compactness and packing coefficient strictly vary depending on the chemical composition [14- 16].
According to the hypothesis expressed by A.F. Ioffe [21], short-range order in the arrangement of atoms plays a decisive role in the formation of the structure of the band spectrum of condensed matter. So, we can come to the conclusion that changes in short-range order parameters observed depending on the chemical composition should also be reflected in optical transitions, which if we take into account that optical phenomena are controlled by the energy spectrum of electrons. Thus, studies of the optical properties of chalcogenide glasses differing in chemical composition will undoubtedly be useful in explaining the mechanism of optical phenomena occurring in them, as well as their suitability for practical purposes. As a result of these we conclude that multicomponent chalcogenide glasses are suitable, consisting of elements with different coordination numbers, which make it possible to obtain information about the correlation between the parameters of short-range order and local structure. The object of study of the presented work (As-Ge-Se(Te)) consists of elements with coordination numbers 4 (Ge), 3(As) and 2 (Se(Te)), which satisfies the above requirements.
The purpose of this work is to study the optical properties of the As–Ge–Se (Te) system and identify the correlation between short-range order features and optical, as well as other physical parameters. 
 

Experiments

The synthesis of Ge-As-Se(Te) compositions was carried out in the following sequence: highly pure elemental substances (Ge, As, Te) in the required atomic percentages were filled into quartz ampoules have internal diameter of 12 mm and after air was pumped out to a pressure of 1.33×10−4 Pa to prevent oxidation of materials and within 3 hours they were heated to a temperature of ~900 °С and kept for about 12 hours at this temperature. The synthesis was carried out in a rotating furnace in order to ensure the homogeneity of samples and cooling was carried out in the off furnace mode. Films of thicknesses 1 µm used in research were obtained by thermal evaporation at a rate of 0.3µm/min onto glass substrates in vacuum at a pressure of 1.33×10−4 Pa. Thicknesses of films were measured with an MII-4 optical microscope. Densities of chalcogenide glasses, ρ were calculated using the formula:

                  (1)

Where 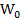 and 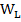 the weight of the sample in air and in liquid (water) and density ( ) of liquid (water) is equal to 1 g/cm³ at room temperature. The density of glass materials was measured by Archimedes' principle using liquid (water). The accuracy was better than ±0.02 g/cm³. The amorphous properties of thermal evaporated films were proved by X-ray diffraction analysis by using D8-Advance powder diffractometer. Amorphous of chalcogenide glass substances was proved by wide maxima observed in the diffraction.

Results and discussion

To determine the optical band gap, the transmission spectra of the As–Ge–Se(Te) glass systems were measured in the region of high absorption coefficients (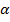 ). The values ​​of α were calculated using the formula  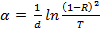and the results obtained in the form of the dependence of  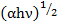on the photon energy (hν) are presented in figure 1. In the formula written above R and T are the reflection and transmission coefficients of studied thin films, but d is thickness of films. The linear dependence of  on the photon energy (hν) in a sufficiently wide interval indicates that the electronic transitions correspond to indirect allowed transitions in the studied materials. The optical band gap (Eg) is determined by extrapolating the linear part of the curves to zero absorption and   results obtained in the form of the dependence of Eg on the parameters Z and R are presented in figure 2. As can be seen from the figure Eg decreases for compositions with selenium (Se), but value of Eg for compositions with telluriuma slight increase is observed with an increase in Z (figure 2a) and a decrease in R (figure 2b).

Figure 1. Optical absorption spectra of As-Ge-Se (a) and As-Ge-Te (b) chalcogenide glass systems

Full size image

The average coordination number (Z) and numerical values ​​of the R- parameter were calculated based on the following formulas (2), (3) in order to investigate the correlation between the optical properties and local structure of studied substances.

   (4)

In formulas (2), (3) ,  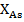and 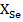 are the molar fractions of elements included inchalcogenide glasses composition.

Figure 2. Dependences of the optical band gap of As-Ge-Se (Te) chalcogenide systems on Z (a) and R (b)

Full size image

To explain the observed changes in the optical band gap depending on the chemical composition (on the parameters Z and R) of the materials studied, one should take into account the peculiarities of the dependence of such parameters as the packing coefficient (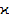 ) and the average atomic volume ( 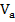) on these parameters, as well as the nature of their formation zone structure. Numerical values ​​of density ( 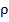), the values ​​of  and  were calculated for all compositions by using the experimentally results and following formulas (4), (5).

    (4)

   (5)

Where 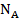 is the number Avagadro's, 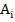,  are the atomic mass and molar fraction of the elements included in glass compositions. The obtained results in the form of a curves dependence of these values ​​on Z (a) and R (b) are presented in figure 3 and figure 4.

Figure 3. Dependence of packing coefficient of As-Ge-Se (Te) glass systems on Z (a) and R (b)

Full size image

Figure 4. Dependence of average atomic volume of As-Ge-Se(Te) glass systems on Z(a) and R(b)

Full size image

According to the idea put forward by the author of work [22] on the nature of the band structure of chalcogenide glass materials, according to which, when atoms are bonded in a solid, the valence band is formed by lone pair electronic states (LP electron states) and conduction bands are formed by antibonding states (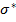 -antibonding states) states. The values ​​of the optical band gap (Eg) correspond to the energy distances between the upper boundaries of the LP states and the bottom of the  states. Changes in the energy positions of these states should be reflected in values of optical band gap (Eg). It is advisable to associate the energy positions of these states, as well as the observed changes in the band gaps depending on the chemical composition and changes of the atomic packing coefficients (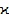 ) and average atomic volume ( ). As can be seen in figure 3 and 4, the dependences of 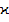,  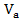on Z and R are non-monotonic and exhibit extremum at values ​​of Z and R corresponding to the stoichiometric compositions ( ). Moreover, changes in Z and R have different effects on the values ​​of the indicated parameters for the systems included selenium and tellurium. As a result an increase value of average coordination number (Z) and a decrease of R- parameterare observed increase value of  and a decrease of  for As-Ge-Se chalcogenide glass system. In contrast to above in As-Ge-Te atomic packing coefficients (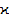 ) decreases, but average atomic volume ( ) increases. This fact indicates that short-range order effects in As-Ge-Se are more pronounced than in the As-Ge-Te system, which is explained due to high chemical activity of selenium relative to tellurium. It is believed that interatomic electromagnetic interaction increases with increasing Z (decreasing R) in As-Ge-Se chalcogenide glass system and as a result of which the states σ* are even more separated from each other. Contrary to these results the electromagnetic interaction between atoms weakens in the As-Ge-Te system and indicated σ*-states are closer to each other. Thus, the lower boundary of the conduction band for As-Ge-Se composition shifts downward, which leads to a decrease in the value of the optical band gap (Eg). The lower boundary of the conduction band shifts up in the As-Ge-Te composition, which leads to an increase in the optical band gap (Eg). The features observed in the second section of curves presented in figure 3 and figure 4 apparently occur as a result of changes in the degree of disorder depending on the chemical composition. The extremums of curves in figure 3 and figure 4 correspond to the stoichiometric composition , where the values ​​of the parameters Z and R are 2.5 and 1, which correspond to the chemical threshold value [23]. As already noted [23], the amorphous matrix of a sample corresponding to a chemical threshold is formed mainly from fully cross-linked tetrahedral (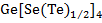 ) and pyramidal ( ) structural units.  In this case amorphous matrix is formed mainly from fully 3D structural units. It is believed that at values ​​of coordination number Z=2.5, a completely is ​​formed cross-linked three-dimensional matrix and 2D→3D structural transition occurs. According to [24], a fully cross-linked three-dimensional matrix corresponds to the chemical composition when the atoms that make up the substance have the largest average volume. In this case, such physical parameters as the density of the substance [23] and packing density (figure 3) should have a minimum value, which was actually observed.

Conclusion

The optical band gap (Eg) was determined by applying the Taus's method to optical absorption spectrum of As-Ge-Se(Te) glass systems. Decreases of optical band gap (Eg) have been established that with an increase of average coordination number (Z) and decrease of parameter- R for compositions containing selenium. But, for glasses containing tellurium the value of Eg slightly increases by increase of average coordination number (Z) and decrease of parameter- R. Changes occurring in values of Eg depending on the chemical composition are explained taking into account the nature of the band spectrum of chalcogenide glass materials, as well as an analysis of experimental facts on the dependences of Eg on Z and R. The non-monotonic nature of the dependence of  and  on Z and R and appearance of extremums at values ​​Z = 2.5 and R=1 corresponding to stoichiometric compositions ( ) were associated with the existence of a chemical threshold at which the 2D→3D structural transition occurs.

References

About this article