Construction of an inhomogeneous solution for the problem of torsion of a radially inhomogeneous transversal isotropic cylinder

Abstract

Introduction

Studying the problem of torsion of radially inhomogeneous transversally isotropic cylinders based on three-dimensional equations of elasticity theory is a labor-intensive task. The analysis of the problem of torsion of a radially inhomogeneous transversely isotropic cylinder is reduced to the study of boundary value problems for a second-order partial differential equation with variable coefficients. These coefficients include elastic moduli, which are arbitrary continuous functions of the radius of the cylinder. This complicates the construction of solutions to torsion problems.
A number of studies are devoted to the study of elasticity theory problems for a radially inhomogeneous cylinder [1, 2]. In [3, 4], the torsion problem and the axisymmetric problem of elasticity theory for a radially layered cylinder were studied. A possible violation of the Saint-Venant principle in its classical formulation is shown. In [5, 6], based on the asymptotic integration method, axisymmetric problems of the theory of elasticity for a radially inhomogeneous cylinder of small thickness were studied in the case where the elastic moduli vary along the radius according to a linear law. In [7, 8], problems of the theory of elasticity for a radially inhomogeneous cylinder of small thickness were studied. An analysis of the stress-strain state determined by homogeneous solutions is carried out. In [9], the Almansi-Michell problem for an inhomogeneous anisotropic cylinder was studied using a numerical-analytical method. In [10], the influence of material inhomogeneity on the stress-strain state of an inhomogeneous orthotropic cylinder was studied. In [11], an asymptotic theory of a transversally isotropic cylinder of small thickness was developed.
In this work, a special solution of the equilibrium equation is established for the torsion problem of a transversely isotropic radially inhomogeneous cylinder when a smooth load is applied on its side surface. For this purpose, the following issues are considered:
- by the asymptotic integration method, a special solution of the equilibrium equation describing the torsion of the cylinder satisfying the given boundary condition on the lateral surface of the cylinder is established; 
- The algorithm for determining the specific solution of the equilibrium equation is given when the stress on the lateral surface of the cylinder is polynomially dependent on the coordinate along the axis of the cylinder.

Construction of an inhomogeneous solution by asymptotic integration method

Let us consider the torsion problem for a radially inhomogeneous transversely isotropic cylinder of small thickness. Let us relate the cylinder to the cylindrical coordinate system 

The equilibrium equations in the absence of mass forces in a cylindrical coordinate system have the form [12]:

    (1)

where   are the components of the stress tensor, which are expressed through the components of the displacement vector as follows [13]:

   (2)

Let’s substitute (2) into (1):

   (3)

Here - displacement vector component; -new dimensionless variables, small parameter characterizing the thickness of the cylinder, elastic characteristics considered as an arbitrary piecewise continuous function of a variable - some characteristic module, for example 

Let us assume that a load is applied to the side of the boundary

    (4)

Here  - fairly smooth functions.

Let us consider the construction of partial solutions of equation (3) that satisfy the boundary conditions (4), that is, inhomogeneous solutions. When constructing particular solutions (3), various techniques can be used. If the thickness of the shell is sufficiently small, and the load specified on the side surfaces is sufficiently smooth and has the order of   relative to the   , then it is advisable to use the asymptotic method to construct inhomogeneous solutions [14].

We will look for solution (3), (4) in the form:

        (5)

Substitution of (5) into (3), (4) leads to a system whose sequential integration over   gives relations for the expansion coefficients 

   (6)

Where

Using the generalized Hooke's law and (5), (6) for stresses , one can obtain asymptotic expressions.

Construction of exact partial solutions of equilibrium equations for special types of loads

Let us construct inhomogeneous solutions for problems (3), (4) using the method described in [15]. We assume that the following boundary conditions are specified on the lateral surfaces of the cylinder:

       (7)

Having a set of solutions for various integers “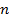 ”, it is possible to construct solutions for arbitrary boundary conditions specified by smooth functions  , having previously approximated them by polynomials.

Let us first consider an auxiliary problem. We assume that the load on the side surfaces is given:

       (8)

We will look for solution (3), (8) in the form:

     (9)

After substituting (9) into (3), (8) we obtain

          (10)

           (11)

where 

The solution (10), (11) is a meromorphic function of the spectral parameter 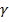, and its poles coincide with the spectrum of the homogeneous problem when 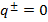.Note that 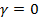is a double point in the spectrum of a homogeneous problem (when ). In the vicinity of zero, solution (10), (11) has the form:

 (12)

Let's introduce the operator:

       (13)

If we apply the operator   to the right-hand side of (8), we obtain the expression on the right-hand side of (7). Let's substitute (12) into (9), and then into (3), (8). Next, we act on (3), (8) with the operator (13) and equating the coefficients at the same powers of , we obtain a recurrent system of boundary value problems for determining  :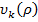

        (14)

          (15)

 (16)

where  - Kronecker symbol, .

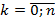          The solution to problem (3), (7) takes the form:

      (17)

The system of boundary value problems (14)-(16) is effectively solved by the small parameter method. Let us construct a solution in the case of 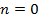 (constructing a solution for has no fundamental difficulties):

       (18)

Constants 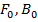 are determined when the boundary conditions at the ends of the cylinder  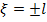are satisfied.

Results and discussion

An inhomogeneous solution is established for the torsional problem of a radially inhomogeneous transverse-isotropic cylinder of small thickness. It is assumed that the elastic moduli are arbitrary continuous functions depending on the radius. Considering that the formulated boundary value problems include a small parameter characterizing the thickness of the cylinder, the first asymptotic process of the method of asymptotic integration of elasticity theory equations is used to construct an inhomogeneous solution. The resulting asymptotic formulas are suitable as .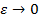 
An algorithm for determining the specific solution of the equilibrium equation is given when the stress on the lateral surface of the cylinder is given as a polynomial dependence on the coordinate along the axis of the cylinder. 
From the solutions established above, non-homogeneous solutions are obtained for torsion problems of a radially non-homogeneous isotropic cylinder and a homogeneous transverse isotropic cylinder in a special case.

Conclusion

Inhomogeneous solutions have been constructed for the problem of torsion of a radially inhomogeneous transversely isotropic cylinder of small thickness, i.e. partial solutions of equation (3) satisfying boundary conditions (4) were constructed. A method is shown for constructing partial solutions of equilibrium equations when the lateral surface of a cylinder is loaded with forces that depend polynomially on the axial coordinate. The resulting asymptotic formulas for displacement make it possible to calculate the stress-strain state in a radially inhomogeneous transversely isotropic cylinder of small thickness with any predetermined accuracy.

References

About this article